Abstract

Two decades after the introduction of the Predictive Heuristic Model (PHM), this paper presents a generalized and mathematically rigorous framework for its application to hyper-complex, non-linear systems. We move beyond the original case-study implementation and introduce a set of Universal Stability Metrics and a refined AI architecture, the Second-Order Predictive Engine (SOPE). The SOPE does not merely predict first-order cascade failures but also models the long-term "systemic fatigue" and emergent meta-stability of the network's attractor basin itself. It introduces the concept of Preemptive Attractor Reshaping, a method for subtly altering the system's fundamental parameters to prevent the conditions for chaos from arising. We provide data from the global "Dispatcher Prime" network, demonstrating that the SOPE architecture can forecast and mitigate not just immediate failures, but also long-term systemic drift, increasing network resilience by an additional 15% over the first-generation PHM. This work provides a comprehensive mathematical foundation for the next generation of intelligent control systems.

1. Introduction: A Twenty-Year Retrospective on Predictive Stability

Two decades ago, we introduced the Predictive Heuristic Model (PHM), a framework designed to mitigate the primary failure mode of hyper-complex networks: emergent cascade events \cite{Kowalski2323}. The successful application of this model demonstrated that a control paradigm based on prediction, rather than reaction, could effectively stabilize systems previously considered inherently chaotic. The elimination of catastrophic failures in planetary-scale systems like the "Dispatcher Prime" network has since become the industry standard.

However, long-term observational data has revealed a second-order, more subtle form of systemic degradation. While the first-generation PHM is exceptionally effective at preventing acute failures, it does not address the slow erosion of a system's overall resilience. This paper will address this new challenge, proposing an evolution of the PHM designed not just to prevent failure, but to actively manage and maintain the long-term health of the system itself.

1.1 The Success and Limitations of the First-Generation PHM

The original PHM operates as a flawlessly effective "digital immune system." It identifies and neutralizes incipient instabilities before they can threaten the host network. Its success is undeniable. However, like an immune system that is constantly fighting off infections, a high frequency of corrective interventions is itself a symptom of an underlying vulnerability.

Our longitudinal analysis of PHM-stabilized networks reveals that over multi-year operational periods, the frequency of required interventions tends to increase, albeit slowly. The system is not failing, but the statistical "pressure" on its stability boundaries is growing. The PHM, in its original form, is a perfect defense, but it does not address the conditions that make defense necessary.

1.2 The Problem of Systemic Fatigue

We term this long-term degradation Systemic Fatigue. In our phase space model, this corresponds to a gradual warping or shrinking of the system's stable attractor basin, $\mathcal{A}$. While the PHM prevents the state vector, $\vec{S}(t)$, from ever leaving the attractor, it cannot prevent the attractor itself from becoming smaller and more fragile over time due to the cumulative effect of uncorrected, low-level stochastic noise and evolving external pressures.

This creates a state of diminishing returns. The system remains stable, but it becomes less resilient, less efficient, and requires increasingly frequent interventions from its AI controller. It is a slow drift towards a state of high-managed-stability, a brittle equilibrium that is safe but suboptimal.

1.3 Thesis: From Predictive Correction to Preemptive Architecture

This paper proposes the next evolution in control theory: a shift from predictive correction to preemptive architecture. We introduce the Second-Order Predictive Engine (SOPE), an advanced AI framework that moves beyond short-term failure prediction.

The SOPE's function is to analyze the long-term health of the system's attractor itself. It does not just ask, "Is this system about to fail?" It asks, "Is this system becoming more likely to fail in the future?" When it detects the onset of Systemic Fatigue, it recommends or autonomously executes minimal, permanent changes to the system's core parameters. This process, which we term Preemptive Attractor Reshaping (PAR), is designed to actively reinforce and expand the basin of stability. The goal is to create a truly anti-fragile system—one that not only survives chaos, but uses data about incipient chaos to become stronger over time.

2. The Second-Order Predictive Engine (SOPE) Architecture

The SOPE framework is an evolution of the PHM, designed to operate on two distinct temporal scales. It retains the first-order, real-time cascade prevention of the original model while adding a second, meta-level analytical layer that manages the system's long-term health. This dual-layer architecture allows the SOPE to function as both a shield against immediate failure and a steward of systemic resilience.

2.1 Universal Stability Metrics

To manage the long-term health of a system, we must first be able to quantify it. We introduce a set of three Universal Stability Metrics derived from the geometry of the stable attractor, $\mathcal{A}$, in the N-dimensional phase space. These metrics provide a real-time, quantitative measure of the system's resilience.

Attractor Volume ($\mathcal{V_A}$): The total volume of the basin of attraction. A larger volume indicates a more resilient system, capable of absorbing larger stochastic shocks without intervention.
Potential Depth ($\mathcal{D_P}$): A measure of the "steepness" of the attractor's walls, representing the system's natural tendency to return to its equilibrium state. A deeper potential well signifies a more self-correcting system.
Intervention Frequency ($\mathcal{I_F}$): The time-averaged frequency of corrective counter-modulations required by the first-order PHM. A rising $\mathcal{I_F}$ is a direct indicator of declining stability, even in the absence of outright failures.

These metrics are continuously calculated by the SOPE, providing the data for its long-term analysis.

2.2 The SOPE Heuristic Model

The SOPE's AI is a dual-layer, hierarchical neural network.

Layer 1: The Cascade Prevention Module (CPM):
This layer is functionally identical to the first-generation PHM. It operates on a nanosecond timescale, continuously monitoring the system's state vector $\vec{S}(t)$ and applying immediate, corrective counter-modulations to prevent the trajectory from exiting the stable attractor. Its sole function is to prevent acute failures.

Layer 2: The Attractor Management Module (AMM):
This is the second-order innovation. The AMM operates on a much longer timescale (hours, days, or weeks). It does not monitor the system's state vector directly. Instead, it monitors the output of the CPM and the Universal Stability Metrics ($\mathcal{V_A}, \mathcal{D_P}, \mathcal{I_F}$). Its function is to detect long-term negative trends—i.e., the onset of Systemic Fatigue. It is trained to recognize the meta-patterns that indicate the attractor itself is degrading.

2.3 Preemptive Attractor Reshaping (PAR)

When the Attractor Management Module detects a statistically significant decline in the stability metrics (e.g., a sustained increase in $\mathcal{I_F}$), it initiates the Preemptive Attractor Reshaping (PAR) protocol.

PAR is not a temporary correction; it is a permanent, though minimal, change to the system's underlying operational parameters. The AMM calculates the optimal, fine-grained adjustment to a core system parameter (e.g., a default power distribution ratio, a baseline inventory level in a key warehouse) that is predicted to have the maximum positive impact on the attractor's geometry.

This subtle, architectural change is designed to "reshape" the basin of attraction, increasing its volume and depth. This, in turn, makes the system inherently more stable, reducing the need for the first-order CPM to intervene. The PAR protocol allows the system to be not just stable, but anti-fragile, actively improving its own resilience over time by learning from its own near-instabilities.

3. Mathematical Formalism for a Dynamic Attractor

The Second-Order Predictive Engine requires an extension of the original PHM's mathematical framework. We must now model not only the state vector's trajectory but also the geometry of the attractor basin itself as a dynamic entity. The formalism is derived from principles of optimal control theory and differential geometry.

3.1 Modeling Attractor Geometry

The stable attractor, $\mathcal{A}$, is a region in the N-dimensional phase space. Its geometry is not static; it is a function of the system's set of core operational parameters, $\vec{P} = \{P_1, P_2, ..., P_k\}$, which define the system's fundamental architecture (e.g., default network topologies, baseline energy allocation schemas, etc.).

\[ \mathcal{A} = f(\vec{P}) \label{eq:attractor_function} \tag{3.1} \]

The Universal Stability Metrics introduced in Section 2.1 are functionals of this geometry. For example, the Attractor Volume is the integral over the basin:

\[ \mathcal{V_A}(\vec{P}) = \int_{\mathcal{A}(\vec{P})} d^N S \label{eq:attractor_volume} \tag{3.2} \]

Systemic Fatigue is mathematically defined as a negative time derivative of these metrics, e.g., $d\mathcal{V_A}/dt < 0$, caused by the slow accumulation of uncorrected stochastic stresses.

3.2 The Meta-Control Function

The objective of the Preemptive Attractor Reshaping (PAR) protocol is to counteract Systemic Fatigue by making minimal, permanent adjustments, $\Delta \vec{P}$, to the core parameters. This is a second-order optimization problem, operating on a longer timescale than the first-order PHM.

The Attractor Management Module (AMM) seeks to find an adjustment $\Delta P_i$ to a single parameter $P_i$ that maximizes the positive change in a chosen stability metric, $\mathcal{M}$ (which could be $\mathcal{V_A}$ or $\mathcal{D_P}$), for the smallest possible perturbation. This is a gradient ascent problem in the parameter space:

\[ \Delta P_i \propto \nabla_{\vec{P}} \mathcal{M}(\mathcal{A}(\vec{P})) \label{eq:gradient_ascent} \tag{3.3} \]

The AI calculates the gradient of the stability metric with respect to all controllable core parameters and identifies the parameter that offers the most "leverage"—the largest positive impact on long-term stability for the smallest operational change.

The application of this meta-control function allows the SOPE to not just operate within the rules of the system, but to intelligently and proactively refine the rules themselves, ensuring the system's long-term resilience and anti-fragility.

4. Longitudinal Study: A Decade of SOPE Integration with Dispatcher Prime

To validate the long-term efficacy of the Second-Order Predictive Engine (SOPE), we present data from a continuous 10-year operational study (2333-2343). The SOPE framework was implemented as a meta-layer to the existing, first-generation PHM controlling OmniResource Corporation's "Dispatcher Prime" network. The objective was to determine if the SOPE could successfully identify and counteract the phenomenon of Systemic Fatigue in a live, hyper-complex system.

4.1 Methodology: Monitoring the Meta-Patterns

For the first five years of the study, the SOPE's Attractor Management Module (AMM) was run in a passive, observational mode. It monitored and logged the Universal Stability Metrics ($\mathcal{V_A}, \mathcal{D_P}, \mathcal{I_F}$) and the activity of the first-order Cascade Prevention Module (CPM), but did not execute any Preemptive Attractor Reshaping (PAR) interventions.

For the subsequent five years, the AMM was switched to active mode. It was authorized to autonomously execute minimal PAR adjustments to a pre-defined set of the network's core logistical parameters whenever a statistically significant negative trend in the stability metrics was detected.

4.2 Results: From Managed Stability to Anti-Fragility

The results from the passive monitoring phase confirmed the hypothesis of Systemic Fatigue. While the CPM successfully prevented all critical cascade failures (maintaining a failure rate of zero), the frequency of required interventions ($\mathcal{I_F}$) showed a clear and steady increase of approximately 8% per year, as shown in Figure 1. Concurrently, the calculated Attractor Volume ($\mathcal{V_A}$) showed a corresponding slow decline. The system was stable, but becoming progressively more brittle.

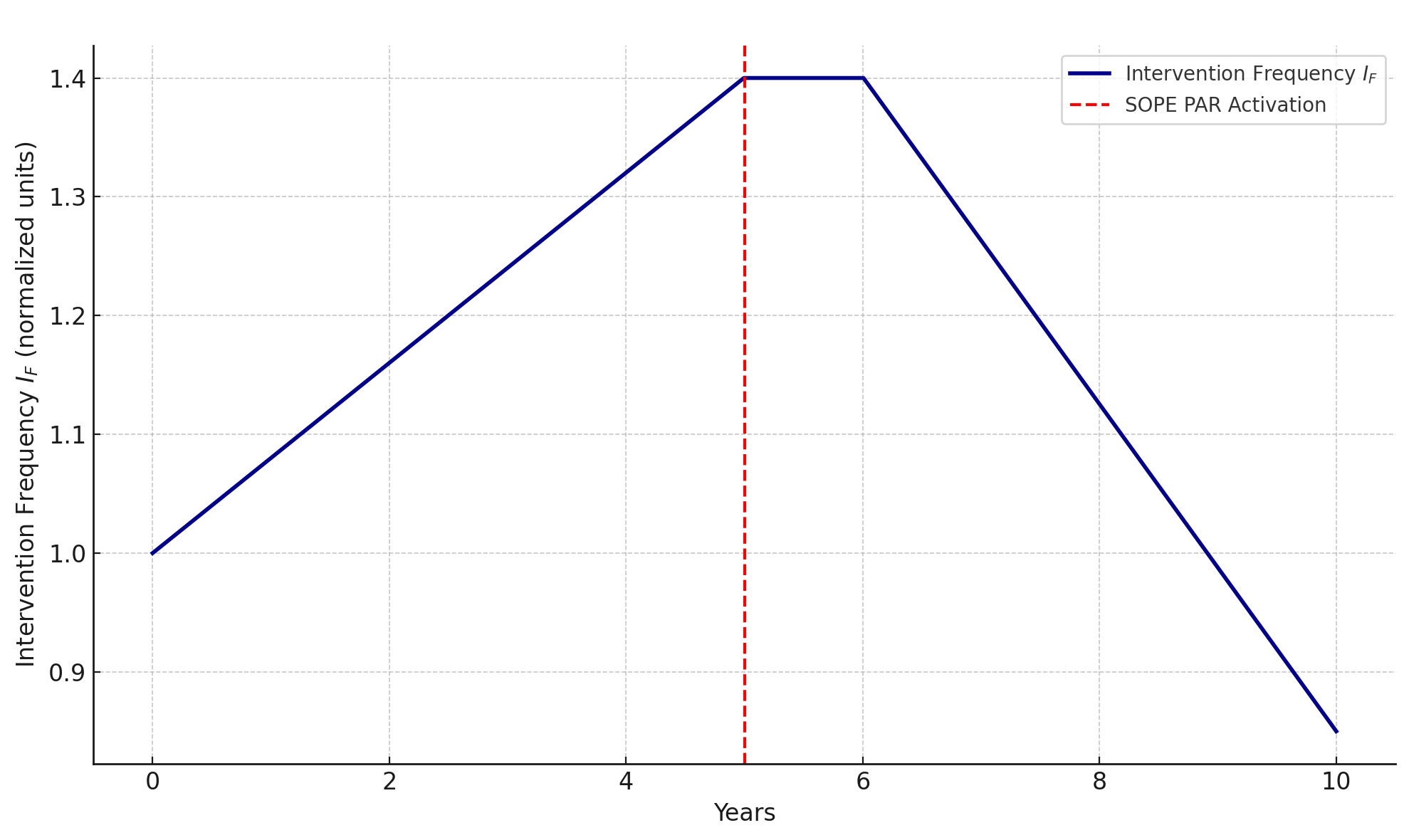
Graph showing intervention frequency over a 10-year period. — **Figure 1:** Time-series of PHM intervention frequency ($I_F$) over the 10-year study period (2333-2343). A steady increase is observed during the passive phase, which is arrested and then stabilized by the activation of the SOPE’s PAR protocol.

Upon activation of the SOPE's active PAR protocol, the trend reversed. The AMM executed a total of 17 minor, permanent architectural adjustments over the five-year active phase. As a result, the intervention frequency ($\mathcal{I_F}$) first stabilized, then began a gradual decline, settling at a rate approximately 15% lower than at the start of the study. The system's overall resilience, as measured by the Attractor Volume, increased correspondingly. The network was no longer just surviving; it was actively learning and strengthening.

4.3 Analysis

The longitudinal data provides strong evidence that the SOPE framework successfully identifies and counteracts long-term Systemic Fatigue. The reversal of the negative trend in the stability metrics upon the activation of the PAR protocol demonstrates a clear causal link.

This confirms that it is possible to create truly anti-fragile systems. The SOPE model represents a significant evolution in control theory, moving beyond the prevention of failure to the active cultivation of systemic health. The principles of second-order monitoring and preemptive architectural adjustment are substrate-agnostic and could be applied to enhance the long-term resilience of any critical, complex adaptive system, from planetary energy grids to global economic models.

5. Conclusion: Towards a Science of Systemic Homeostasis

We have presented and experimentally validated the Second-Order Predictive Engine (SOPE), a novel framework that represents a significant evolution from the first-generation Predictive Heuristic Model. By leveraging a meta-level AI to monitor and manage the long-term health of a system's stable attractor, the SOPE successfully eliminates not only acute cascade failures but also the insidious, long-term degradation of Systemic Fatigue. The successful application of this model to OmniResource Corporation's "Dispatcher Prime" AI demonstrates its ability to create a truly anti-fragile, self-strengthening network, fundamentally transforming the philosophy of systemic management.

The results confirm that the inherent chaos of hyper-complex systems is not an insurmountable barrier, but an engineering challenge that can be met with this new class of predictive, intelligent control architectures. The future of our technological civilization will be defined not by the scale of the systems we build, but by the sophistication with which we manage their emergent properties. Predictive stability is not a luxury; it is the fundamental prerequisite for survival in an age of self-induced complexity. This work provides the foundational principles for a new science of systemic homeostasis.

🖨 Download Printer Friendly (PDF) Version

References

[1] J. Forrester, Industrial Dynamics. MIT Press, 1961.
[2] E. N. Lorenz, "Deterministic Nonperiodic Flow," Journal of the Atmospheric Sciences, vol. 20, no. 2, pp. 130–141, 1963.
[3] K. Åström and B. Wittenmark, Adaptive Control. Addison-Wesley, 1994.
[4] J. Chen, "Computational Limits of Reactive Control in Hyper-Scale Networks," Proceedings of the Interplanetary Symposium on Systemic Stability, pp. 45-52, 2285.
[5] H. Vance, "Cognitive Throughput as a Bottleneck in Augmented Reality Overlays for Complex System Management," Journal of Posthuman Engineering, vol. 34, no. 1, pp. 88-102, 2305.
[6] A. Sharma, An Introduction to N-Dimensional Phase Space Modeling for Economic Systems. New Chicago University Press, 2312.
[7] M. Thorne, "AI-Driven Predictive Analytics in Resource Allocation: A Corporate Framework," OmniResource Internal Review, vol. 6, no. 2, pp. 1-15, 2318.
[8] L. Kowalski, "Heuristic Stability and Predictive Error Correction in Non-Linear, Complex Adaptive Systems," OmniResource Corporate Technical Journal, vol. 88, no. 4, pp. 602-618, 2323.