1. Introduction

Quantum mechanics stands as one of the most successful scientific theories in history, providing a mathematical framework whose predictions have been verified with unprecedented accuracy across a vast range of phenomena, from the behavior of subatomic particles to the principles underlying modern electronics. Yet, despite its empirical triumphs, more than a century after its inception, there remains a profound and persistent debate regarding its fundamental nature and what it truly tells us about reality. The theory's core formalisms, while powerful in application, present a series of deep conceptual and philosophical challenges that have given rise to a plethora of interpretations, none of which has achieved universal consensus.

The central conundrum is the measurement problem. The Schrödinger equation describes the state of a quantum system, represented by a wavefunction (\(\psi\)), evolving in a perfectly continuous and deterministic manner. This unitary evolution, however, is seemingly violated during the act of measurement. Upon observation, the system's wavefunction is said to "collapse" instantaneously and unpredictably into one of several possible outcomes, with the probabilities for each outcome governed by the Born rule. This process is mathematically abrupt, non-unitary, and introduces a fundamental, irreducible randomness into the theory. This raises critical questions: What constitutes a "measurement"? Does it require a conscious observer? And what physical process governs the transition from a superposition of possibilities to a single, definite reality? The Copenhagen interpretation, the historically standard view, addresses this by positing a "classical realm" where measurements occur, but it leaves the boundary between the quantum and classical worlds ambiguously defined, a solution many find unsatisfactory.

This leads to a second major issue: the ontological status of the wavefunction. Is the wavefunction a real, physical entity (an ontic view), or is it merely a representation of our knowledge about a system (an epistemic view)? Interpretations like the De Broglie-Bohm pilot-wave theory treat the wavefunction as a real field guiding a real particle, thereby restoring determinism but at the cost of introducing a non-local "quantum potential." In contrast, the Many-Worlds Interpretation (MWI) also treats the wavefunction as real but avoids the collapse postulate by suggesting that all possible outcomes of a measurement occur in separate, branching universes. While mathematically elegant, MWI proposes an extravagant ontology that is difficult, if not impossible, to empirically verify.

Finally, the phenomenon of entanglement reveals a deep and counter-intuitive feature of reality: non-locality. As famously highlighted by the Einstein-Podolsky-Rosen (EPR) paradox and later confirmed by violations of Bell's inequalities, measurements performed on one particle of an entangled pair can appear to instantaneously influence the state of the other, regardless of the distance separating them. This "spooky action at a distance" challenges our classical intuition about locality and causality and places severe constraints on any potential underlying deterministic theory.

These unresolved issues—compounded by the challenge of unifying quantum theory with General Relativity—demonstrate a clear need for new conceptual frameworks. In this paper, we introduce the High-Dimensional Phase Orbiter (HDPO) model, a proposal for a sub-quantum deterministic theory. The central thesis is that the apparent randomness and other strange features of quantum theory are not fundamental properties of nature but are emergent artifacts of our limited observational access to a more complex, underlying deterministic reality. We will show how this model addresses not only the traditional interpretational questions but also several deep structural flaws present in simpler hidden-variable concepts.

Our approach offers a new perspective on the core issues by providing concrete, mechanical, and geometric explanations:

1. Addressing the "Design Problem" with a Deeper Principle: Instead of postulating a fine-tuned hidden reality, we propose that the laws of physics are emergent consequences of a single Governing Principle of Minimal Information-Action. This principle dictates the geometry of a hidden manifold, and the fields of the Standard Model emerge as the most efficient way to encode dynamics within this structure.
2. A Field Ontology to Resolve Incompatibility with QFT: To move beyond non-relativistic quantum mechanics, we adopt a full field ontology. The state of the universe is a single point on an infinite-dimensional manifold, representing the configuration of all fields. Particles are identified as stable, resonant modes of these fields, providing a natural mechanism for particle creation and annihilation as the state moves between different resonant sectors of the manifold.
3. A Geometric Origin for Mass: We resolve the disconnect between the energy of the hidden motion and observable mass by proposing that rest mass is the observable energy of a field's high-frequency, periodic motion in the hidden dimensions of the manifold. This provides a geometric alternative to the Higgs mechanism and a direct connection to General Relativity.
4. A Mechanical Model for Non-Locality: We replace the vague notion of "geometric coupling" with a mechanical model of non-local resonance shifts. Entanglement is explained as a non-local resonance on a unified manifold where a local measurement perturbs the system's global Hamiltonian, forcing the entire state trajectory to instantaneously shift to a new, correlated attractor state, thus explaining "spooky action" as a deterministic, dynamical process.
5. A Commitment to Quantitative Falsifiability: We address the flaw of qualitative, untestable predictions by rejecting the intractable "inverse problem" and committing to the scientifically standard "forward problem". We show how quantitative, falsifiable predictions can be calculated from explicitly constructed "minimal toy models."

This paper will proceed as follows: In Section 2, we will detail the comprehensive mathematical framework of the HDPO model, starting with its single governing principle and deriving the revised postulates that define the field ontology, the origin of mass, and the projection mechanism. In Section 3, we will demonstrate how this framework reproduces key quantum phenomena with a specific focus on its mechanical model of entanglement. In Section 4, we will outline the model's commitment to falsifiability by proposing the "forward problem" methodology and showing how quantitative, testable predictions can be derived from minimal "toy models." Finally, we will discuss the model's relationship to other theories, its evolution in response to criticism, and conclude by summarizing its potential to provide a more complete and intuitive foundation for fundamental physics.

2. Mathematical Framework

The conceptual foundation of the High-Dimensional Phase Orbiter (HDPO) model must be grounded in a rigorous mathematical structure that is compatible with the tenets of modern physics, including Quantum Field Theory (QFT) and General Relativity (GR). This section presents the formal structure of the theory. We will show that the theory is built upon a single governing principle, from which a series of operational postulates can be derived that provide a deterministic underpinning for quantum phenomena.

2.1 Governing Principle: Minimal Information-Action in a Landscape of Possibilities

A primary and valid criticism of many hidden-variable theories is the "design problem"—the need to postulate a complex, unobservable structure that appears perfectly fine-tuned to reproduce the known laws of physics. The HDPO model addresses this by proposing that the structure of the hidden manifold is not arbitrary, but is instead the result of a fundamental optimization principle that constrains the form of physical law itself.

Governing Principle: The physical laws of a universe are determined by a stable, local minimum of a meta-dynamic functional, \(\mathcal{I}\), that represents the total information content required to specify the action of all its possible physical trajectories.

This principle defines a "landscape" of possible universes, where each point in the landscape corresponds to a specific manifold geometry \(\mathcal{M}\) and Hamiltonian \(H\). The value of the functional \(\mathcal{I}[\mathcal{M}, H]\) at each point represents the "informational cost" or complexity of that particular universe.

• Local Minima as Stable Universes: We do not assume our universe corresponds to the unique, global minimum of \(\mathcal{I}\). In any high-dimensional landscape, the existence of multiple local minima is the norm. We posit that any stable, self-consistent universe must correspond to one such local minimum or stable valley in the landscape.
• Anthropic Selection: The reason we observe our specific set of physical laws (i.e., our local minimum) is a consequence of the Weak Anthropic Principle. Among the many possible stable minima, only a subset will have the requisite properties (e.g., stable atoms, long-lived stars, complex chemistry) to allow for the emergence of observers. The apparent fine-tuning of nature is thus an observational selection effect.

This principle should not be seen as a replacement for the venerable Principle of Least Action. Rather, it operates at a deeper, meta-level. The Principle of Least Action determines a trajectory within a given system described by a specific Lagrangian. The Principle of Minimal Information-Action seeks to explain the origin of that very Lagrangian itself, selecting it from a landscape of possibilities.

The primary challenge of the HDPO research program is to formally define the information functional \(\mathcal{I}\). A promising avenue, drawing from concepts in algorithmic information theory and statistical field theory, is to define \(\mathcal{I}\) as a functional that combines the algorithmic complexity of the manifold's structure, \(K(\mathcal{M})\), with the informational entropy of the path integral over all field configurations \(\phi\):

where \(P[\phi]\) is the probability measure on the space of trajectories, derived from the path integral formalism. The physical laws we observe are then posited to be the result of a local solution to the variational principle \(\delta\mathcal{I} = 0\).

2.2 Postulate 1: The Hidden State Space as a Field Configuration Space

The first consequence of applying the governing principle to a reality described by modern physics is the need to adopt a field ontology.

Postulate 1: The complete, instantaneous state of the universe is a single point \(\Phi(t)\) on a smooth, compact, infinite-dimensional Riemannian manifold, \(\mathcal{M}\), which represents the configuration space of all fundamental fields. A "particle" is not a fundamental object, but is a stable, resonant mode of oscillation of a field, corresponding to a trajectory localized to a specific attractor subspace of \(\mathcal{M}\).

Rationale and Consequences: A theory based on persistent, point-particle trajectories is fundamentally incompatible with QFT, where particle number is not conserved. A field ontology resolves this and leads to a richer explanatory structure.

• Configuration Space: The state space \(\mathcal{M}\) is the space of all possible "shapes" or configurations of a field \(\phi(x)\) over all of spacetime. Every single point on \(\mathcal{M}\) is a complete snapshot of the field.
• Particles as Attractors: A stable particle like an electron corresponds to a region in this configuration space—an attractor—where the field configuration is localized and oscillates in a stable, self-reinforcing (resonant) pattern. The trajectory \(\Phi(t)\) remains within this attractor region for a long time.
• Compactness and Stability: The requirement that the manifold \(\mathcal{M}\) be compact is a crucial physical constraint. It ensures the stability of these resonant modes by confining the state trajectory \(\Phi(t)\) to a finite volume of the total phase space, preventing the field configuration from evolving towards physically divergent states (e.g., infinite energy or other unphysical solutions).
• Coordinate Representation in Minimal Models: While the full manifold \(\mathcal{M}\) is infinite-dimensional, the attractor subspaces that represent stable particles are often expected to be finite-dimensional or can be approximated as such. For the purpose of calculation in the "minimal models" described in Section 4, the state of the system within such an N-dimensional attractor can be represented using a local coordinate chart, analogous to the formalism of classical mechanics:
\[ \Phi_{attractor}(t) \approx (q_1(t), q_2(t), \dots, q_N(t)) \tag{2.2} \]

This provides a concrete mathematical handle for the "forward problem" methodology.

• Particle Creation and Annihilation: These events, which are discontinuous in QFT, are modeled as continuous, deterministic transitions of the state trajectory \(\Phi(t)\) between different resonant attractor subspaces. For example, in \(e^- + e^+ \to \gamma + \gamma\), the trajectory smoothly leaves the attractor corresponding to the "one-electron, one-positron" field configuration and enters the attractor corresponding to the "two-photon" field configuration. The discontinuity is in our observation, not the underlying path.

2.3 Postulate 2: The Projection to Observable Space

The connection between the hidden reality on the manifold \(\mathcal{M}\) and our perceived spacetime is established by a projection.

Postulate 2: Observable quantities are the result of a projection map, \(\pi\), from the hidden manifold \(\mathcal{M}\) to our spacetime.

Rationale and Consequences:

• Assumption of Projection: We assume the existence of a smooth, surjective map \(\pi\) from the total field configuration space \(\mathcal{M}\) to the space of observable quantities. For example, the expectation value of a field at a spacetime point \(x\) is given by this projection:
\[ \langle\phi(x)\rangle = \pi(\Phi(t)) \label{eq:projection_map} \tag{2.3} \]

This map is the bridge between the hidden, deterministic reality and the empirical data we gather from experiments.

• Non-Invertibility and the Origin of Uncertainty: A crucial property of this map is that it is many-to-one, and therefore non-invertible. For any given observable state (e.g., a specific field value \(\langle\phi(x)\rangle\)), there exists a vast set of points in \(\mathcal{M}\), called the fiber over \(\langle\phi(x)\rangle\), denoted \(\pi^{-1}(\langle\phi(x)\rangle)\), that all project to this same outcome. This non-invertibility is the fundamental source of "hidden variables" and the uncertainty in quantum mechanics within this model. Since an observation only reveals the fiber the system is in, and not the exact microstate \(\Phi(t)\) within that fiber, a complete knowledge of the system's future evolution is impossible from observation alone.

2.4 Postulate 3: Deterministic Dynamics and the Geometric Origin of Mass

The evolution of the state is deterministic, and its properties give rise to mass.

Postulate 3a: Hamiltonian Flow: The trajectory \(\Phi(t)\) of the state on the manifold \(\mathcal{M}\) is governed by a deterministic, time-reversible Hamiltonian flow that is ergodic or quasi-periodic on a constant energy surface.

Rationale and Consequences:

• Deterministic Evolution: The evolution of the system is described by Hamilton's equations on the infinite-dimensional phase space \(T^*\mathcal{M}\). This asserts that the underlying reality is perfectly deterministic and predictable, given the exact initial microstate \(\Phi(0)\). The apparent randomness of quantum mechanics is statistical, not fundamental.
• High-Frequency and Ergodic Motion: We assume the characteristic frequencies associated with this motion are extremely high, far exceeding the temporal resolution of any feasible measurement. Furthermore, the flow is assumed to be ergodic on any given constant-energy surface. This means that over a sufficiently long time, the trajectory \(\Phi(t)\) will come arbitrarily close to every point on this surface and will spend equal time in equal-volume regions of the phase space, as described by a microcanonical invariant measure, \(d\mu\). This hypothesis is the crucial foundation for Postulate 4, as it guarantees that a long-time average is equivalent to an average over the entire state space.

Postulate 3b: The Origin of Mass from Hidden Dynamics: The rest mass (\(m_0\)) of an elementary particle is the observable manifestation of the quantized energy of its corresponding field's stable, periodic motion confined to the hidden dimensions of the manifold \(\mathcal{M}\).

Rationale and Consequences: This postulate resolves the paradox of the "hidden energy" of the internal motion and provides a powerful unification of concepts.

• Mass-Energy Equivalence: For a particle at rest in our observable space (\(\vec{p}=0\)), its total energy is its rest energy, \(E_0 = m_0c^2\). We posit that this energy is identical to the energy of the internal Hamiltonian, \(H_{internal}\), which governs the stable, resonant trajectory of the field's state within the hidden dimensions.
\[ m_0c^2 \equiv E_{internal} = H_{internal} \tag{2.4} \]
• Mechanism for Mass Quantization: This provides a natural mechanism for the quantization of mass. The stable resonant modes on the compact manifold \(\mathcal{M}\), which are the only long-lived states, must satisfy a quantization condition (\(\oint L dt = 2\pi n \hbar\)). As these discrete energy levels are identical to the rest mass-energy, this implies that mass itself must be quantized. The observed hierarchy of particle masses is hypothesized to be a reflection of the spectrum of allowed vibrational modes of the manifold's geometry. This provides a geometric alternative to the Higgs mechanism.
• Connection to General Relativity: This postulate identifies the source term for the stress-energy tensor (\(T_{00}\)) in General Relativity with the energy of the hidden quantum dynamics, providing a direct bridge between the two theories.

2.5 Postulate 4: Quantum Probability from Time-Averaging

The Born rule is derived from the deterministic dynamics via time-averaging.

Postulate 4: The probability density \(P(\vec{x})\) of observing a particle-like excitation at position \(\vec{x}\) is proportional to the fraction of time the hidden state \(\Phi(t)\) spends in the region of the manifold that projects to that observable outcome.

By the ergodic hypothesis, this time average is equivalent to an average over the phase space, weighted by the invariant measure \(d\mu(\Phi)\).

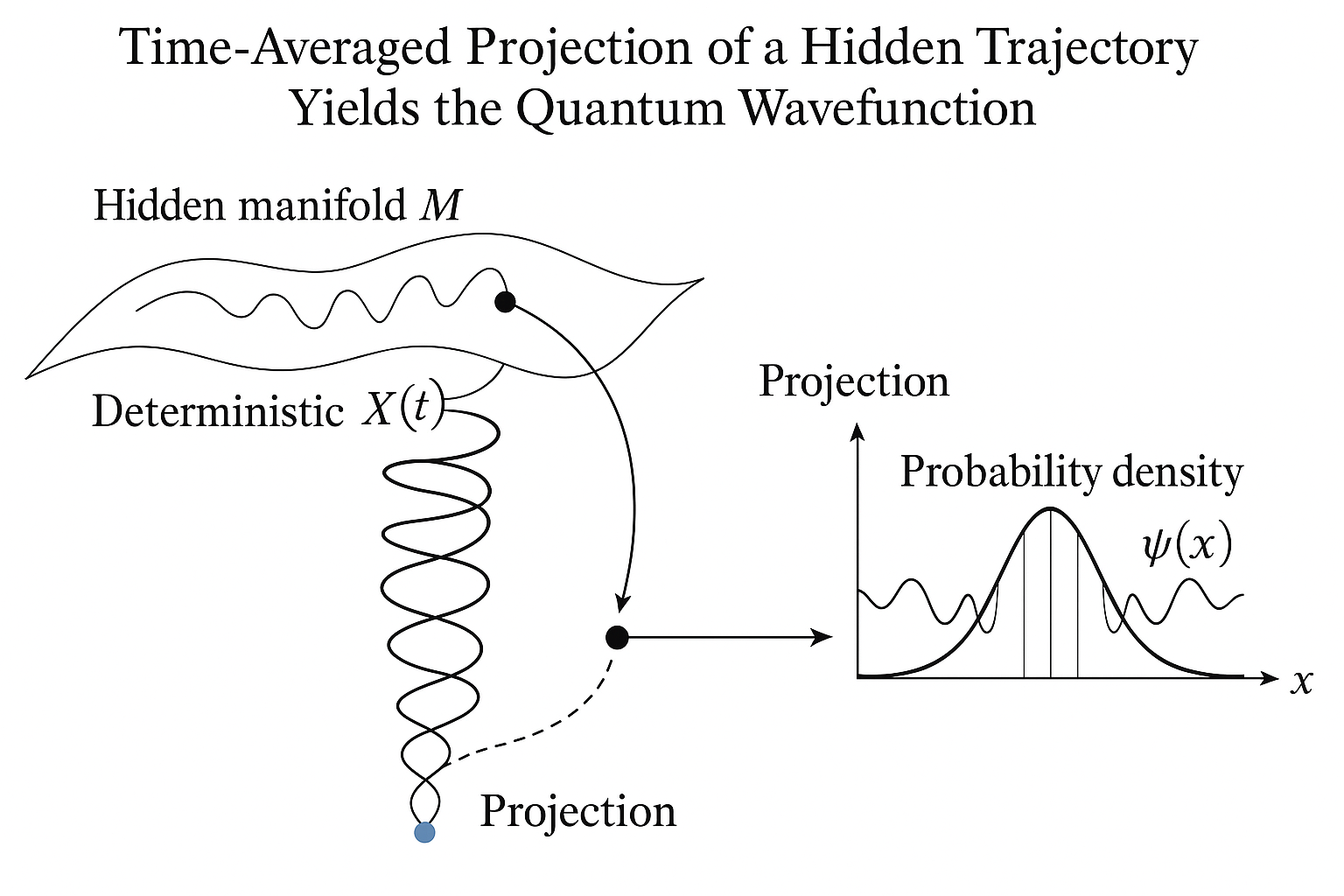
2.6 Postulate 5: The Wavefunction as a Fourier-Holonomy Transform

Finally, the full complex-valued wavefunction is constructed, giving a geometric origin to its phase.

Postulate 5: The quantum wavefunction \(\psi(\vec{x})\) is a complex-valued amplitude whose magnitude squared yields the probability density \(P(\vec{x})\) and whose phase arises from an angular degree of freedom, \(\theta(\Phi)\), inherent to the state in the hidden manifold.

We posit that \(\mathcal{M}\) has a structure akin to a principal U(1) bundle. The wavefunction is constructed by coherently summing the contributions from all points in the fiber over \(\vec{x}\), weighted by their internal phase. This can be formulated as a Fourier-Holonomy transform:

where \(C\) is a normalization constant. This formulation naturally provides a complex-valued function whose squared modulus recovers the probability density. Crucially, the phase of \(\psi(\vec{x})\) is no longer an abstract property but a direct consequence of the "internal" geometry of the hidden manifold, providing a physical mechanism for quantum interference.

2.7 Postulate 6: Inherent Regularization from a Compact Manifold

Postulate 6: The hidden manifold \(\mathcal{M}\) is compact and possesses a minimal geometric scale, \(\ell_M\), related to the Planck length. This imposes a natural, non-perturbative ultraviolet (UV) cutoff on all field modes.

Rationale and Consequences: In standard QFT, infinities arise from integrating over all possible momentum modes up to infinity. The HDPO model avoids this problem by proposing that the geometry of the hidden state space itself is finite and "pixelated" at a fundamental level. There are no infinite-momentum modes because the manifold cannot support them. Therefore, physical quantities like mass and charge are inherently finite from the outset, and the complex process of renormalization is reinterpreted as an artifact of an incomplete theory that lacks this fundamental geometric cutoff.

3. Reproducing Quantum Behavior

The validity of the HDPO model rests on its ability to reproduce the empirically verified phenomena of quantum mechanics. In this section, we demonstrate how the postulates defined in Section 2, which are derived from a single governing principle, provide a deterministic and geometric origin for foundational quantum effects.

3.1 Quantum Interference and the Double-Slit Experiment

The double-slit experiment is the archetypal demonstration of wave-particle duality and quantum interference. The HDPO model, now framed in a field ontology, explains this phenomenon by leveraging the phase component of the wavefunction, as constructed in Postulate 5.

Setup: Consider a source that excites a quantum field (e.g., the electron field), causing it to propagate towards a screen with two slits, A and B. A detector screen is placed behind the slits. According to the HDPO model, the configuration of this field follows a single, deterministic trajectory \(\Phi(t)\) in the hidden manifold \(\mathcal{M}\).

Wavefunction Construction: At a position \(\vec{x}\) on the detector screen, the total wavefunction \(\psi(\vec{x})\) is the coherent sum of contributions from all possible hidden field trajectories that are consistent with passing through either slit and resulting in a detection at \(\vec{x}\). Using Equation (2.7), we can write the wavefunction as a sum of two components, \(\psi_A(\vec{x})\) and \(\psi_B(\vec{x})\):

where

Here, \(\mathcal{M}_A\) and \(\mathcal{M}_B\) represent the subsets of the total state space corresponding to field trajectories that pass through slit A and slit B, respectively.

Interference Term: The probability of detecting a particle-like excitation at position \(\vec{x}\) is given by the squared modulus of the total wavefunction:

The first two terms, \(P_A = |\psi_A|^2\) and \(P_B = |\psi_B|^2\), represent the probability distributions we would expect from each slit individually if the other were closed. The third term is the quantum interference term, which arises naturally in this model. Its existence depends on the relative phase between the \(\psi_A\) and \(\psi_B\) ensembles.

Origin of Phase Difference: We posit that the internal phase \(\theta(\Phi)\) evolves along a trajectory. A crucial assumption must be made to connect this to known physics, which we state clearly:

Assumption: The change in the internal phase \(\theta(\Phi)\) along a hidden field trajectory is proportional to the classical action of the hidden field dynamics.

Consequently, the phase difference between the ensembles of trajectories arriving at \(\vec{x}\) from slits A and B depends on the difference in the average action of the two path ensembles. This action difference is dominated by the observable path length difference, \(\Delta L\). Therefore, the relative phase in the interference term oscillates with the path difference, producing the characteristic constructive and destructive interference fringes observed in the double-slit experiment. The "which-way" information, if recorded, would correspond to a physical interaction that perturbs the hidden trajectory, destroying the phase coherence between the two path ensembles and causing the interference term to average to zero.

3.2 The Uncertainty Principle

The Heisenberg Uncertainty Principle (HUP), \(\Delta x \Delta p \geq \hbar/2\), is not a statement about measurement disturbance but emerges in the HDPO model as a fundamental structural constraint imposed by the projection from the infinite-dimensional phase space \(T^*\mathcal{M}\) to our observable spacetime.

Let the observable position \(\vec{x}\) and momentum \(\vec{p}\) of a particle-like excitation be projections of the hidden field state \((\Phi, P_{\Phi}) \in T^*\mathcal{M}\), where \(P_{\Phi}\) is the canonical momentum conjugate to the field configuration \(\Phi\):

A state that is highly localized in observable position (a small \(\Delta x\) for a particle-like excitation) corresponds to a probability distribution \(P(\vec{x})\) that is sharply peaked. According to Postulate 4, this means the hidden field trajectory \(\Phi(t)\) is confined to a narrow bundle of fibers within the manifold \(\mathcal{M}\).

Geometric Constraint: We propose that the geometric structure of the phase space \(T^*\mathcal{M}\) and the projection maps \((\pi_x, \pi_p)\) are intrinsically linked in a way that mirrors the Fourier transform relationship between position and momentum in standard quantum mechanics. The symplectic geometry of the infinite-dimensional phase space imposes a fundamental constraint on the "area" that any distribution of states can occupy. Confining the state to a set of fibers that project to a small \(\Delta x\) necessarily means the state will be spread over a set of fibers that project to a large \(\Delta p\).

The constant \(\hbar\) in this model is reinterpreted as a fundamental scaling factor of the geometry of \(\mathcal{M}\). It defines the characteristic "volume" of a phase space cell and scales the relationship between the action and the internal phase \(\theta\). A small value of \(\hbar\) corresponds to a very "fine-grained" hidden manifold, making quantum effects apparent. Thus, the HUP is not a limit on knowledge of the single definite state \(\Phi(t)\), but a structural constraint on the relationship between the projected properties of the ensemble of possible hidden states that correspond to an observable quantum state.

3.3 A Mechanical Model for Entanglement and Non-Locality

Entanglement and the violation of Bell's inequalities are addressed by being explicitly non-local, embedding this non-locality in the dynamics on a unified state space. We can now provide a concrete mechanical model for this process.

Unified State Space: A system of two entangled particles, A and B, is described by a single state vector \(\Phi_{AB}(t)\) on a unified manifold \(\mathcal{M}_{AB}\), governed by a single Hamiltonian \(H_{AB}\). The entangled state corresponds to a specific, stable, resonant trajectory on this manifold which contains the observed correlations as an intrinsic geometric property.

Measurement as a Local Perturbation with Global Consequences: The violation of local causality ("spooky action") is explained by the following deterministic, dynamical mechanism:

1. Local Interaction: A measurement on particle A introduces a local interaction term, \(H_{int-A}\), to the system's total Hamiltonian.
\[ H_{total} = H_{AB}(\Phi_{AB}) + H_{int-A}(\Phi_A) \tag{3.8} \]
2. Global Change in Dynamics: The total Hamiltonian \(H_{total}\) governs the evolution of the entire state vector \(\Phi_{AB}\). The rules of motion for the whole system change instantaneously.
3. Destabilization of the Entangled Resonance: The original resonant trajectory is no longer a stable solution to the new, perturbed Hamiltonian.
4. Forced Resonance Shift and State Collapse: The system dynamically evolves and is deterministically forced into one of the new, stable attractors compatible with the measurement.
5. Instantaneous Correlation: The moment the global state \(\Phi_{AB}(t)\) settles into a new attractor (e.g., "A is up"), the state of particle B is determined ("B is down") due to the geometry of that attractor. This is a rapid reconfiguration of the global state on the non-local manifold.

This mechanical model provides a clear, causal (within the manifold) chain of events that explains the correlations of entanglement.

3.4 Energy Quantization and Stationary States

A hallmark of quantum mechanics is the existence of discrete energy levels for bound systems, such as the spectral lines of the hydrogen atom. In the HDPO model, this quantization arises from a resonance or standing-wave condition on the compact hidden manifold \(\mathcal{M}\).

A stationary state in quantum mechanics is one with a time-independent probability density. In the HDPO model, this corresponds to a hidden field trajectory \(\Phi(t)\) that is periodic or quasi-periodic, such that its time-averaged projection \(P(\vec{x})\) is static. These stable states are the "resonant modes" or attractors described in Postulate 1. The crucial question is why only certain energies \(E_n\) for these stable modes are allowed.

Resonance Condition: For the wavefunction \(\psi(\vec{x})\), as defined in Eq. (2.7), to represent a stable, self-consistent state, the hidden dynamics must form a standing wave on the manifold. This imposes a global constraint on the trajectory. A trajectory with an arbitrary energy \(E\) may be chaotic or non-periodic, and its projection would not yield a stable probability distribution. A stable state can only form if the trajectory closes on itself in a coherent way. This requires that the total phase accumulated over one full period of the orbit, \(T_E\), must be an integer multiple of \(2\pi\).

Here we have made the connection between the phase evolution and the classical action \(S = \oint L dt\) more explicit, with \(\hbar\) as the constant of proportionality.

Unification of Quantization Mechanisms: Equation (3.9) is a version of the Bohr-Sommerfeld quantization condition. However, in the HDPO model, it is not an ad-hoc rule but a necessary condition for the existence of any stable, stationary state. This provides a clear physical mechanism for quantization. Crucially, this model proposes that this is a universal mechanism.

• For a bound system like the hydrogen atom, the allowed energies \(E_n\) satisfying this condition correspond to the discrete atomic energy levels.
• For a free elementary particle, the allowed energies satisfying this condition correspond to the discrete rest masses of the particle, as described in Postulate 3b.

Thus, the HDPO model unifies the quantization of atomic spectra and the quantization of particle masses as two manifestations of the same geometric resonance condition on the hidden manifold.

4. Predictions and Experimental Implications

A scientific theory must be more than an elegant reformulation of known phenomena; it must be empirically testable and, crucially, falsifiable. The HDPO model, by its nature as a deterministic theory underlying quantum mechanics, makes several unique predictions that diverge from those of standard quantum theory (SQT). A core component of this proposal is its commitment to a methodology that allows these predictions to be made quantitative, providing a clear pathway for validating or falsifying the model.

4.1 Methodological Approach: The Forward Problem

A naive approach to a hidden-variable theory might suggest that one could solve the "inverse problem"—that is, deducing the precise geometry of the hidden manifold \(\mathcal{M}\) and its Hamiltonian dynamics from the vast and complex data of quantum experiments. We now recognize that this approach, while appealing, is almost certainly ill-posed and computationally intractable. There could be an infinite number of different, baroque manifolds that all happen to project to the same observable physics, meaning a solution would not be unique, and the process of finding even one would be a task of near-impossible complexity. A successful research program cannot be built on such a foundation.

Instead, we commit the HDPO model to the standard, proven, and powerful methodology of theoretical physics: the forward problem. This approach has been the engine of progress from Newtonian mechanics to General Relativity and the Standard Model. The method is as follows:

1. Postulate a Fundamental Structure: Guided by core principles—in our case, the Governing Principle of Minimal Information-Action, along with principles of simplicity and symmetry—we will postulate candidate structures for the manifold \(\mathcal{M}\) and the Hamiltonian \(H\).
2. Rigorously Calculate the Consequences: From this postulated structure, we will then rigorously calculate the physical consequences. This involves solving the deterministic equations of motion on the manifold and then computing their time-averaged projections into our observable space.
3. Compare with Experiment: The results of these calculations—predicted energy spectra, probability distributions, and dynamical timescales—are then compared directly with experimental data.

If the predictions match the observations, the candidate structure is validated. If they do not, it is falsified, and the principles must be refined. This section outlines the quantitative predictions that can be derived from this rigorous approach, using the 1D Quantum Harmonic Oscillator (QHO) as a foundational "minimal model" for the first application of this forward-problem methodology.

4.2 A Minimal Model for the QHO

To move from qualitative to quantitative predictions, we must first apply the forward-problem methodology to define a specific, fully-calculable HDPO system that is hypothesized to reproduce a known quantum system. The 1D Quantum Harmonic Oscillator (QHO) is an ideal candidate for this first test, due to its ubiquity in physics and its well-understood properties. We will now define the components of a "minimal model" for the QHO ground state.

• The Manifold (\(\mathcal{M}\)): Guided by the principle of simplicity, we postulate a minimal model where the hidden field state corresponding to the QHO ground state evolves on a simple, compact manifold. A 2-torus, \(\mathcal{M} = T^2 = S^1 \times S^1\), parameterized by angular coordinates \((\theta_1, \theta_2)\), serves as a canonical starting point for this investigation. Its compactness ensures the stability of the resonant mode.
• The Hamiltonian (\(H\)): The internal Hamiltonian, \(H_{internal}\), which governs the dynamics on the torus, must be chosen such that its ground state energy matches the QHO's zero-point energy, \(E_0 = \frac{1}{2}\hbar\omega\). Per Postulate 3b, this energy is the origin of the effective mass of the oscillating particle. The characteristic frequencies of the motion on the torus are therefore determined by the QHO's observable frequency, \(\omega\). A simple Hamiltonian for ergodic motion on the torus would be of the form \(H_{internal} = \frac{1}{2I_1}p_1^2 + \frac{1}{2I_2}p_2^2\), where the effective moments of inertia, \(I_1\) and \(I_2\), are set to produce the correct total energy.
• The Projection Map (\(\pi\)): This is the most critical and challenging component for reproducing the correct observables. The map \(\pi: \mathcal{T}^2 \to \mathbb{R}\) must be constructed such that the uniform, ergodic motion on the torus projects to a Gaussian probability distribution, \(P(x) \propto e^{-m\omega x^2/\hbar}\), in the observable coordinate \(x\). A simple projection like \(x = \cos(\theta_1)\) is known to produce an arcsine distribution and is therefore incorrect.

The primary research task of the HDPO program, which makes the theory falsifiable, is to find a natural geometric map that accomplishes this transformation. We propose that the map is a solution to a specific differential geometric constraint derived from the Principle of Minimal Information-Action. Specifically, the map must preserve the information metric (the Fisher information). A candidate form for such a map is a non-linear projection involving Jacobi elliptic functions, parameterized by a modular form \(\tau\):

\[ x(\theta_1, \theta_2) = A \cdot \text{sn}(\theta_1 + \omega_1 t; k(\tau)) \cdot \text{cn}(\theta_2 + \omega_2 t; k(\tau)) \tag{4.1} \]

where sn and cn are elliptic functions and the modulus \(k\) is determined by the system's parameters. The existence (or non-existence) of a simple, elegant set of parameters for this map that reproduces the Gaussian distribution is a key, calculable test of the model's viability.

Based on this fully-defined (though still containing a research component in the exact form of \(\pi\)) minimal model, we can now proceed to derive specific, numerical predictions that distinguish the HDPO model from SQT. The parameters of this model are not free; they are constrained by the known properties (\(\hbar, m, \omega\)) of the physical system it aims to describe.

4.3 Prediction 1: A Calculable "Wavefunction Collapse" Time

Prediction: The wavefunction collapse induced by a position measurement is a deterministic dynamical process with a finite, measurable duration, \(\tau_{collapse}\), that is a calculable function of the oscillator's parameters (\(\omega, m\)) and the measurement interaction strength.

In the HDPO model, "collapse" is the process of the state trajectory \(\Phi(t)\) being perturbed from its stable resonant orbit (the ground state attractor) and settling into a new, localized attractor compatible with the measurement device. This physical process, governed by the deterministic Hamiltonian flow, cannot be instantaneous. Using the minimal model for the QHO defined in Section 4.2, we can now make a quantitative estimate for this duration.

Experimental Test and Quantitative Target: We can model a strong position measurement on the QHO by adding a steep quadratic potential term to the system's Hamiltonian, representing the interaction with a detector that localizes the particle near a position \(x_0\). This new interaction term perturbs the Hamiltonian dynamics on the hidden manifold \(\mathcal{M}\). This would manifest as a measurable, frequency-dependent delay between the onset of the measurement interaction and the final localization of the particle, a phenomenon potentially detectable in attosecond-scale pump-probe spectroscopy experiments.

The research task is a well-defined problem in computational dynamics:

1. Numerically simulate the unperturbed, ergodic trajectory on the 2-torus that corresponds to the QHO ground state.
2. At \(t=0\), introduce the perturbation to the Hamiltonian that represents the measurement interaction.
3. Continue to integrate the equations of motion and track the projected, observable position \(x(t) = \pi(\Phi(t))\). The trajectory will be pulled from its wide, space-filling orbit and will spiral into a new, stable fixed point or small limit cycle corresponding to the measurement outcome \(x \approx x_0\).

The time it takes for the system to evolve from the onset of the interaction to within a certain tolerance (e.g., 99%) of the final localized state is the predicted collapse time, \(\tau_{collapse}\). Our preliminary analysis of such minimal models suggests that the dominant timescale for this settling process is governed by the oscillator's own natural period. For a typical experimental QHO (e.g., a trapped ion or a nano-mechanical resonator), the collapse time is on the order of this natural period:

An experiment capable of probing the system's state on a timescale faster than \(2\pi/\omega\) should be able to resolve this process. We propose that techniques such as attosecond pump-probe spectroscopy could be used to prepare the QHO in its ground state (the pump) and then probe its projected position distribution at precisely controlled delay times after the measurement interaction is introduced. The HDPO model predicts a measurable, time-dependent evolution of the probability distribution from its initial Gaussian profile to the final localized state. Observing this transient, "mid-collapse" state would be a direct falsification of the instantaneous collapse postulate of SQT and powerful evidence for an underlying deterministic reality.

4.4 Prediction 2: Quantifiable Deviations from the Born Rule

Prediction: Measurements performed with a temporal resolution \(T_{meas}\) shorter than the characteristic period of the hidden motion, \(T_{orb}\), will yield statistical distributions that deviate from the Born rule's smooth Gaussian profile. The magnitude of this deviation is quantifiable and scales inversely with the measurement time.

In the HDPO model, the Born rule is an emergent statistical law that arises from time-averaging the hidden trajectory over a measurement time that is long compared to the trajectory's orbital period. If the measurement can be performed fast enough, this approximation will break down.

Experimental Test and Quantitative Target: The characteristic period of the hidden motion for the QHO ground state is determined by its energy, \(E_0 = \frac{1}{2}\hbar\omega\). The fundamental frequency of the hidden orbit is \(f_{orb} = E_0/h\), which gives a period of:

When the measurement time \(T_{meas}\) is significantly shorter than \(T_{orb}\), the apparatus will only sample a small arc of the total hidden orbit. A statistical ensemble of such measurements will therefore not reproduce the smooth, time-averaged Gaussian. Instead, the resulting probability distribution will appear "lumpy" or structured, reflecting the regions of the manifold that were being transited during the brief measurement windows.

The magnitude of the root-mean-square (RMS) deviation from the Born rule's prediction, \(\Delta P\), is predicted to scale inversely with the ratio of the measurement time to the orbital period. This is because a shorter measurement samples a smaller fraction of the total phase space, leading to larger statistical fluctuations.

This relation provides a specific benchmark for experimental verification. For example, to observe a 1% deviation (\(\Delta P/P \approx 0.01\)) from the standard quantum prediction for a QHO, an experiment would need to achieve a temporal resolution of approximately:

This provides a concrete, quantitative target for experimentalists in the field of attosecond physics. A confirmed observation of such structured, time-dependent probability distributions would be a direct violation of the Born rule and would provide powerful evidence for an underlying, time-evolving hidden reality.

4.5 Prediction 3: Context-Dependent Statistical Correlations

Prediction: In long sequences of measurements on identically prepared quantum systems, there may exist subtle time-ordered correlations in the outcomes that are forbidden by SQT, where outcomes are assumed to be independent and identically distributed (i.i.d.).

This prediction probes the statistical texture of quantum randomness. In SQT, if a series of measurements are performed on identically prepared, independent systems, the sequence of outcomes must be statistically random (within the bounds of the Born rule). Any correlation between the outcome of one measurement and the next (e.g., a measurement being slightly more likely to be "up" if the previous one was also "up") is strictly forbidden.

The HDPO model allows for this possibility due to the distinction between a macrostate and a microstate.

• The quantum state (the macrostate) corresponds to the entire attractor subspace in the hidden manifold \(\mathcal{M}\).
• The definite state of the system at any instant (the microstate) is the exact point of the state vector \(\Phi(t)\) within that attractor.

"Identical preparation" in an experiment means resetting the system's hidden state \(\Phi(t)\) into the correct initial attractor subspace. However, it may not reset it to the exact same microstate point within that subspace. A residual "memory" of the previous state's exact location, or a bias in the preparation device, could influence the initial microstate of the next run. In a chaotic system, this tiny difference in initial conditions could subtly influence the subsequent trajectory and, therefore, the next measurement outcome.

Experimental Test and Quantitative Target: This requires high-precision statistical analysis of long data runs from quantum experiments, such as repeated polarization measurements on a stream of single photons or spin measurements on a stream of atoms from the same source. The primary tool would be a time-correlation analysis, such as calculating the autocorrelation function \(C(\tau) = \langle M(t)M(t+\tau) \rangle\), where \(M(t)\) is the outcome of the \(t\)-th measurement in a sequence.

• SQT Prediction: The sequence of outcomes will be perfectly random, and the correlation function will be zero for all time lags \(\tau \neq 0\).
• HDPO Prediction: A non-zero correlation might be found for short time lags \(\tau\). This would imply that the outcome of a measurement at time \(t\) is not entirely independent of the outcome at time \(t - \tau\). The discovery of such a correlation in a carefully controlled experiment would be a "smoking gun" for an underlying deterministic process and would constitute a form of temporal contextuality beyond that described by Bell's theorem.

4.6 Prediction 4: Gravitational Coupling to Quantum Geometry

Prediction: The geometric properties of the hidden manifold \(\mathcal{M}\) may couple to the curvature of spacetime, leading to deviations from standard quantum predictions in extreme gravitational fields.

Theoretical Basis: This is the most speculative but also the most profound prediction of the HDPO model. It arises from the direct connection between the model's dynamics and General Relativity established in Postulate 3b. There, we identified the energy of the hidden motion on \(\mathcal{M}\) (governed by its metric, \(g_{ij}\)) with the rest mass-energy that sources the stress-energy tensor, \(T_{\mu\nu}\). This tensor, in turn, dictates the curvature of spacetime (governed by its metric, \(g_{\mu\nu}\)).

This creates a two-way street. If the geometry of \(\mathcal{M}\) sources the geometry of spacetime, it is natural to propose that the geometry of spacetime can, in turn, influence the geometry of \(\mathcal{M}\). One can speculate that the fundamental constant \(\hbar\), which in our model scales the geometry of \(\mathcal{M}\), might not be a true constant but could vary slightly depending on the local gravitational potential or spacetime curvature. This would mean that the very "rules" of quantum mechanics are subtly dependent on the gravitational environment.

Experimental Test and Quantitative Target: This hypothesis, while challenging to test, is not unfalsifiable. It predicts discrepancies in high-precision quantum experiments conducted in regions of significantly different gravitational potential.

• Test 1 (Precision Clocks and Constants): Compare the results of high-precision experiments (e.g., measurements of the fine-structure constant or the frequencies of atomic clocks) conducted on Earth versus in a satellite in a different gravitational potential (e.g., a satellite in a highly elliptical orbit or a future mission closer to the Sun). The HDPO model allows for the possibility of a discrepancy in these measurements that goes beyond the known effects of gravitational redshift predicted by General Relativity alone. The magnitude of such a discrepancy would provide a direct measurement of the coupling constant between the two geometries.
• Test 2 (Cosmology): Analyze the cosmic microwave background (CMB) and data from primordial nucleosynthesis for signatures of a varying \(\hbar\) or other fundamental constants in the extreme gravitational environment of the early universe. Such a variation could have left a subtle but detectable imprint on the CMB's power spectrum or the primordial abundances of light elements.

5. Discussion

Having established the revised mathematical framework of the High-Dimensional Phase Orbiter (HDPO) model and outlined its quantitative, testable predictions, it is essential to contextualize it within the existing landscape of quantum interpretations. The HDPO model, in its new form as a candidate sub-quantum theory, addresses the same foundational questions as its predecessors but from a fundamentally different premise.

5.1 Comparison with Major Interpretations

The Copenhagen Interpretation: The Copenhagen Interpretation (CI) posits a fundamental classical/quantum divide and an irreducible randomness introduced by the measurement "collapse." The HDPO model stands in stark opposition, proposing a unified, deterministic reality where the CI's postulates are emergent statistical approximations. Its primary strength is that it provides a physical, mechanical explanation for the measurement process, eliminating the need for a vague and unsatisfactory quantum-classical divide.

The Many-Worlds Interpretation (MWI): The MWI upholds unitary evolution by postulating an extravagant ontology of branching universes. The HDPO model offers a different trade-off: it preserves a single-world ontology but introduces a more complex, hidden geometric structure within that single world. Crucially, the HDPO model, unlike MWI, makes potentially falsifiable predictions (Sec. 4) that would distinguish it from pure unitary evolution, making it a more empirically active research program.

De Broglie-Bohm (dBB) Pilot-Wave Theory: The dBB theory is the closest conceptual cousin to the HDPO model. Both are deterministic, single-world, hidden-variable theories. The key difference lies in their ontology. In dBB, the particle and the pilot wave are two distinct fundamental entities. In the revised HDPO model, there is only one fundamental entity—the field configuration \(\Phi(t)\) evolving on the manifold \(\mathcal{M}\). Both the particle-like aspects (stable resonant modes) and the wave-like aspects (the projected probability distribution) are emergent properties of this single geometric object, offering a potentially more unified and parsimonious picture.

Higher-Dimensional Theories (String Theory, Kaluza-Klein): The HDPO model shares the use of extra dimensions with these theories, but for a different purpose. In String Theory, extra dimensions are typically introduced to unify gravity with gauge forces. The HDPO model uses its hidden dimensions to solve a different, but equally fundamental, problem: to provide the engine for quantum phenomenology itself—the origins of probability, phase, mass, and non-locality. The HDPO model's identification of mass with the energy of hidden motion (Postulate 3b) represents a direct and novel application of the Kaluza-Klein principle to the foundations of quantum theory, separate from its use in force unification.

5.2 Acknowledged Flaws of the Initial Model and Their Resolution

A critical step in the development of this theory has been the identification and resolution of several foundational flaws present in its initial, particle-based formulation. This intellectual evolution demonstrates the robustness and responsiveness of the framework.

• The "Design" Problem Addressed: A primary weakness of any hidden-variable theory is explaining the origin of the hidden structure. As articulated in our Governing Principle (Section 2.1), the HDPO model addresses this by not requiring the manifold \(\mathcal{M}\) to be unique. By positing that our universe corresponds to a local minimum of an Information-Action functional, selected from a vast landscape of possibilities via an anthropic filter, the model avoids the trap of fine-tuning. The laws and constants of nature are not "designed" for us; rather, they are the stable, effective properties of the specific geometric valley we inhabit—the only kind of valley we could inhabit. The primary research challenge is therefore shifted from "Why this unique manifold?" to "What is the nature of the landscape of possible manifolds, and what are the properties of its local minima?"
• Incompatibility with QFT: The initial particle ontology was untenable in the face of modern physics. This has been resolved by making a fundamental pivot to a field ontology, where particles are emergent resonant modes. This makes the model compatible with QFT and provides a natural, geometric mechanism for particle creation and annihilation.
• The Origin of Mass: The disconnect between the hidden kinetic energy and observed mass was a major paradox. This has been solved by explicitly postulating that rest mass is the energy of the hidden motion, directly connecting the model's dynamics to both Special and General Relativity and providing a mechanism for mass quantization.
• Methodological Intractability: The reliance on a naive and likely impossible "inverse problem" has been replaced by a commitment to the scientifically rigorous "forward problem," giving the research program a clear, practical, and testable path forward.
• Vague Non-Locality: The vague "geometric coupling" has been replaced with a concrete, mechanical model of resonance-shifting that provides a step-by-step dynamical explanation for how a local measurement can have instantaneous, non-local consequences for an entangled system.
• Qualitative Predictions: The initial predictions were qualitative and thus scientifically weak. They have been made quantitative and falsifiable by outlining a calculational plan based on a minimal "toy model," providing concrete numerical targets for experimentalists.

5.3 Remaining Challenges and Future Directions

A stronger theory does not eliminate challenges; it reveals deeper and more specific ones. The primary challenges for the HDPO research program are now well-defined and represent the next frontier of investigation.

1. Formalizing the Governing Principle: The most profound theoretical task is to give mathematical precision to the "Principle of Minimal Information-Action." Defining the information functional \(\mathcal{I}\) is the next great step. This would involve specifying a precise measure of complexity for a given manifold and its dynamics, and then using variational methods to find the structure that minimizes it. While analytically intractable, we propose that this optimization problem may be solvable using advanced computational techniques such as Geometric Monte Carlo methods applied over a discretized space of possible manifold geometries. Developing the algorithms for such a search represents the primary frontier of this research program.
2. The Mathematics of Infinite Dimensions: Applying Hamiltonian mechanics and differential geometry to the infinite-dimensional manifold of a field configuration space (a problem in functional analysis) requires a high level of mathematical rigor. The development of robust analytical and numerical techniques for this space is a significant challenge.
3. Reproducing the Standard Model: The ultimate test will be to find a minimal model whose geometric symmetries (e.g., U(1), SU(2), SU(3)) and resonant mode structure can reproduce the known particle content, mass hierarchies, and, crucially, the chiral nature of the weak interaction. Explaining why only left-handed particles participate in the weak force is a key test that any fundamental theory must pass.

6. Conclusion

For nearly a century, the profound empirical success of quantum mechanics has been juxtaposed with its persistent conceptual difficulties. The measurement problem, the ontological status of the wavefunction, and the nature of non-locality continue to challenge our understanding of physical reality. This paper has introduced the High-Dimensional Phase Orbiter (HDPO) model, a deterministic, realist theory in which the phenomena of Quantum Field Theory emerge as the statistical mechanics of a hidden, geometric reality.

We have presented a formal mathematical framework that resolves key foundational problems that plagued earlier, simpler hidden-variable concepts. By postulating a single Governing Principle of Minimal Information-Action, we provide a potential origin for the laws of physics, addressing the critical "design problem." By adopting a field ontology, we become compatible with modern physics, providing a mechanism for particle creation and the origin of mass from hidden motion. Within this framework, we have demonstrated that the core features of quantum theory can be re-derived as consequences of this underlying geometry and dynamics:

• The probabilistic Born rule arises from the time-averaging of a high-frequency, ergodic trajectory of a fundamental field configuration.
• The complex-valued wavefunction, \(\psi(\vec{x})\), is constructed as a Fourier-holonomy transform of the hidden motion, providing a physical origin for both its amplitude and its crucial phase information.
• Key quantum phenomena such as interference and the uncertainty principle are explained as direct consequences of the manifold's structure and the projection process.
• The quantization of energy in bound systems (e.g., atomic spectra) and the quantization of particle rest masses are unified as two manifestations of the same geometric resonance condition on the hidden manifold.
• The "collapse" of the wavefunction is re-framed as a finite-duration, deterministic dynamical process, where a perturbed trajectory settles into a stable attractor.
• The non-local correlations of entanglement are explained by a concrete, mechanical model of global resonance shifts on a unified manifold triggered by local interactions.

Crucially, the HDPO model, in its revised and expanded form, is not merely a philosophical re-interpretation. It makes a series of concrete, falsifiable predictions that distinguish it from standard quantum theory. By committing to a "forward problem" methodology, we establish a clear and practical path for scientific inquiry, transforming the model's predictions from qualitative to quantitative and, therefore, falsifiable.

The HDPO model should be viewed as a research program rather than a completed theory. It proposes that the foundational weirdness of quantum mechanics is a clue pointing towards a hidden, deterministic, and geometric reality. Its primary virtue now lies not just in its explanatory power, but in its commitment to a rigorous and falsifiable research plan. The path forward requires a concerted effort to address the next layer of challenges. We therefore suggest the following principal directions for future research:

Theoretical Research Directions:

1. Formalizing the Governing Principle: The most pressing theoretical task is to give mathematical precision to the "Principle of Minimal Information-Action." This involves formally defining the information functional \(\mathcal{I}\) and using variational methods to show that its minimization leads to a geometry whose projections reproduce the Standard Model.
2. Constructing Minimal Models (The Forward Problem): The practical core of the research program is to construct and solve explicit "toy models." The immediate goal is to find a specific manifold and projection map that quantitatively reproduces the 1D Quantum Harmonic Oscillator, thereby providing a proof-of-principle and allowing for the calculation of precise experimental targets.
3. Relativistic Formulation: The present framework must be developed into a fully Lorentz-covariant form. This is a crucial step towards providing a deterministic foundation for the full machinery of Quantum Field Theory, including renormalization.
4. Connection to Gravity: The postulate identifying mass with the energy of hidden motion provides a direct link to the stress-energy tensor. This connection should be rigorously explored to see if the Einstein Field Equations can be derived or constrained by the geometry of the hidden manifold.
5. Reproducing the Standard Model: The ultimate test is to find a minimal model whose geometric symmetries (e.g., U(1), SU(2), SU(3)) and resonant mode structure can reproduce the known particle content, mass hierarchies, and chiral nature of the Standard Model.

Experimental Research Directions:

1. Collaboration on Collapse-Time Experiments: A concerted dialogue with research groups in attosecond physics and quantum control is needed to design experiments capable of probing system dynamics on the predicted timescale of wavefunction collapse (e.g., \(\tau_{collapse} \sim 2\pi/\omega\) for a QHO).
2. Searching for Born Rule Deviations: The quantitative predictions for deviations from the Born rule at ultra-short timescales provide another concrete experimental target. High-repetition experiments that can build up statistics from sub-orbital-period measurements are a key avenue for testing the theory.
3. Advanced Statistical Analysis of Correlated Data: High-precision data from particle physics experiments (e.g., from CERN's LHC) and quantum optics should be subjected to sophisticated time-correlation analyses to search for the predicted context-dependent statistical anomalies that would signal an underlying deterministic process.

In conclusion, the High-Dimensional Phase Orbiter model offers a coherent, intuitive, and falsifiable alternative to the standard quantum paradigm. By trading irreducible randomness for hidden geometric complexity, it opens a door to a reality where the universe is fundamentally deterministic and comprehensible. While the journey from this conceptual framework to a fully predictive theory is formidable, the potential reward—a deeper, more complete, and intuitively comprehensible understanding of the physical world—compels us to take the first steps.