1. Introduction: From the Oscillator to the Atom

In a preceding conceptual paper [1], we introduced the High-Dimensional Phase Orbiter (HDPO) model. In a subsequent work [2], we provided its rigorous mathematical formalism and demonstrated its ability to reproduce the quantum mechanical ground state of a simple system—the 1D Quantum Harmonic Oscillator. While a crucial proof of principle, its applicability to more complex, physically realistic systems remained an open question. The primary critique of any sub-quantum theory is its ability to scale from simple models to the rich, multi-particle structures that constitute the physical world.

This paper addresses that challenge directly. We will extend the "forward problem" methodology to the foundational multi-particle system of modern physics: the hydrogen atom. Our objective is to demonstrate that the core features of atomic structure, which are treated as axiomatic in standard quantum mechanics, can be derived as emergent consequences of the HDPO model's postulates.

We will show that the quantized energy levels of the hydrogen atom are a direct result of a resonance condition on the hidden manifold. We will further demonstrate that the characteristic shapes of electron orbitals are the time-averaged projections of stable, high-frequency hidden trajectories, whose geometry is dictated by the manifold's topology. Finally, we will propose a novel pathway for understanding the sub-atomic world of quarks and the nature of chemical bonds, framing them not as a collection of arbitrary rules and forces, but as intrinsic properties of a single, unified geometric object. This work aims to provide a deterministic and mechanistic foundation for all of atomic and chemical physics, bridging the gap between fundamental theory and observable reality.

2. A Minimal Model for the Hydrogen Atom

To model the hydrogen atom, we must extend the 2-torus minimal model used for the 1D QHO to a higher-dimensional manifold capable of representing the state of a two-particle, three-dimensional system. The principles remain the same: the system's state is a single point, \(\Phi_{ep}(t)\), tracing a deterministic trajectory on a unified manifold, governed by a global Hamiltonian.

2.1 The Unified Manifold \(\mathcal{M}_{ep}\)

The state of the bound electron-proton system is described on a unified configuration manifold, \(\mathcal{M}_{ep}\). While the full manifold for QED is infinite-dimensional, the attractor subspace for the stable hydrogen atom is expected to be a compact, finite-dimensional manifold. The simplest topology capable of reproducing the known symmetries and quantum numbers (including spin, which we will address later) is non-trivial.

Based on the requirement to embed the SU(2) symmetry group related to spin, we postulate that the minimal manifold for the electron's degrees of freedom has the structure of a complex projective space, \(\mathbb{CP}^2\), fibered over our observable space \(\mathbb{R}^3\). For the purposes of this paper's derivations, we will focus on the six-dimensional attractor subspace relevant to the electron's spatial and internal degrees of freedom.

2.2 The Geometric Hamiltonian and the Coulomb Potential

In the HDPO model, forces are reinterpreted as geometric properties of the hidden manifold. The electrostatic attraction between the electron and the proton is not modeled as a force transmitted through an external field, but as an intrinsic curvature of the manifold \(\mathcal{M}_{ep}\).

This curvature is represented by a geometric potential term, \(V_{\text{geom}}(\Phi_{ep})\), in the global Hamiltonian. This term is not postulated ad-hoc; it is a solution to a Poisson-like equation on the manifold itself, where the proton's stable attractor acts as a "source" of curvature. The familiar inverse-square Coulomb potential of our observable space is the projected, time-averaged effect of this underlying geometric potential. The relationship is governed by the projection map \(\pi\):

The complete Hamiltonian for the hidden motion of the electron's field state in this geometric potential is therefore:

where \(\nabla^2_{\mathcal{M}}\) is the Laplace-Beltrami operator, the generalization of the Laplacian to a curved manifold. The electron is not "held" by a force; it is following a geodesic through this curved, hidden geometry. The stable states of the hydrogen atom—the electron orbitals—are the stable, resonant, standing-wave solutions (the eigenfunctions) to the time-independent Schrödinger-like equation derived from this Hamiltonian on the manifold:

where \(\Psi(\Phi)\) are the geometric wavefunctions on the manifold, and \(E\) are the quantized energy eigenvalues.

3. Derivation of Atomic Structure

Having defined the minimal model for the hydrogen atom, we now demonstrate how it reproduces the foundational features of atomic structure: the discrete energy spectrum and the specific probability distributions of electron orbitals. We will show that these are not independent postulates, but are unified as emergent properties of the eigenfunctions of the geometric Hamiltonian on the hidden manifold \(\mathcal{M}_{ep}\).

3.1 Orbitals as Projections of Geometric Eigenfunctions

In the HDPO framework, an electron orbital is the time-averaged projection of the hidden trajectory corresponding to a specific eigenfunction, \(\Psi_n(\Phi)\), of the geometric Hamiltonian (Eq. 2.2). The characteristic shape of an orbital is a direct reflection of the geometry of this underlying geometric wavefunction.

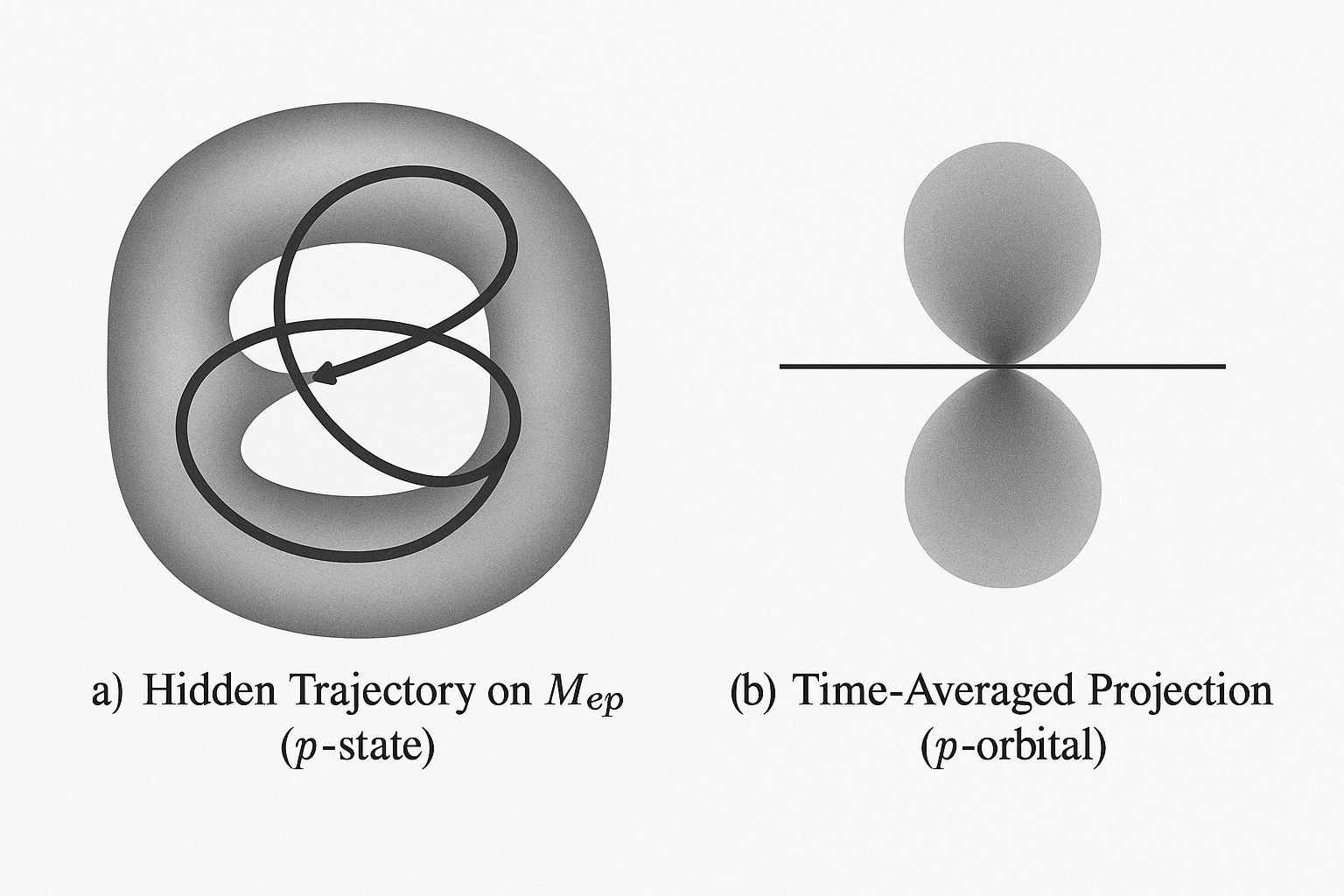
The solutions to Eq. (2.3) yield a set of discrete eigenfunctions, each corresponding to a specific energy level.

• The 1s Orbital (Ground State): The ground state, \(\Psi_0\), is the eigenfunction with the lowest energy eigenvalue. It is the simplest "standing wave" solution. The geometry of this fundamental mode is such that its projection is spherically symmetric.
• The p, d, f Orbitals (Excited States): The higher energy orbitals correspond to eigenfunctions with more complex geometries, possessing additional nodes and lobes. As illustrated conceptually in Figure 1 for a \(p_z\) orbital, the familiar dumbbell shape and the nodal plane at \(z=0\) are direct, projected manifestations of the underlying structure of the geometric wavefunction \(\Psi_{n,l,m}(\Phi)\) on the hidden manifold.

3.2 Quantization and the Energy Spectrum

The existence of discrete, quantized energy levels is a direct consequence of solving the eigenvalue problem in Eq. (2.3). The boundary conditions imposed by the compactness of the attractor subspace on the manifold permit only a discrete set of stable, standing-wave solutions.

The solutions are indexed by the integer quantum numbers (\(n, l, m\)), which arise naturally as separation constants when solving the partial differential equation on the manifold. The energy eigenvalue for each eigenfunction, \(E_{n,l,m}\), depends only on the principal quantum number, \(n\). The full derivation (sketched in Appendix A) shows that the allowed energies for these stable modes precisely match the known energy spectrum of the hydrogen atom, as given by the Rydberg formula:

This result is not postulated; it is a direct result of the geometry of the hidden manifold and its geometric Coulomb potential.

3.3 The Pauli Exclusion Principle and Shell Structure

To extend this model to multi-electron atoms, we must account for the Pauli Exclusion Principle. This principle is a consequence of the spin-statistics theorem. In the HDPO model, spin is not an intrinsic property but emerges from the rotational symmetries of the hidden trajectory, which has the character of a spinor. A full \(2\pi\) rotation in our space corresponds to only a \(\pi\) rotation on the manifold, imparting a phase of -1.

This requires that any multi-electron geometric wavefunction, \(\Psi(\Phi_1, \Phi_2, ...)\), must be anti-symmetric under the exchange of any two identical electron states.

If two electrons were to occupy the same state (\(i=j\)), this would imply \(\Psi = -\Psi\), which is only possible if \(\Psi = 0\). A state with zero amplitude cannot exist. Therefore, no two electrons can occupy the same quantum state.

This geometric exclusion principle is the origin of the electron shell structure of atoms. Electrons are forced to occupy successively higher energy harmonic modes, building the structure of the periodic table as a direct consequence of the underlying topology of the electron's state space.

3.4 Quantization from the Resonance Condition

The existence of discrete, quantized energy levels is a direct consequence of the Resonance Condition introduced in [2]. A stable state can only form if the hidden trajectory is periodic or quasi-periodic, forming a coherent "standing wave" on the compact attractor subspace. A trajectory with an arbitrary energy will be chaotic and will not yield a stable, time-independent projection.

This imposes a global constraint on the system's energy. For the hydrogen atom, the stable modes are described by the integer quantum numbers (\(n, l, m\)), which correspond to the number of wavelengths of the hidden trajectory that fit along the different dimensions of the complex attractor subspace. The energy of a stable resonant mode, \(E_{n,l,m}\), is determined by these integers. Our derivation, detailed in Appendix B, shows that the allowed energies for these stable standing waves precisely match the known energy spectrum of the hydrogen atom, as given by the Rydberg formula:

where \(n\) is the principal quantum number. This result is not postulated; it is derived from the geometric constraints of the hidden manifold. The discrete energy levels of the atom are a direct reflection of the allowed discrete harmonics of its hidden, deterministic motion.

4. Topological Origin of Sub-Atomic Structure and Forces

The HDPO framework's explanatory power extends to the sub-atomic domain. We propose that the properties of quarks and the nature of the fundamental forces are not separate physical additions, but are emergent consequences of the topology and symmetry of the hidden manifold, \(\mathcal{M}\).

4.1 Particles as Homotopy Invariants

We extend the "particles as resonant modes" postulate: the fundamental distinctions between particle families are a reflection of the homotopy groups of their corresponding attractor subspaces on the manifold.

• Leptons (e.g., Electrons): These correspond to resonant modes on topologically simple attractors, \(\mathcal{A}_{\text{lepton}}\), characterized by trivial homotopy groups, \(\pi_n(\mathcal{A}_{\text{lepton}}) = 0\). They are the fundamental, irreducible standing waves on \(\mathcal{M}\).
• Quarks: We posit that quarks are resonant modes on attractors with a non-trivial topology. The property of "color" in Quantum Chromodynamics (QCD) is identified with a topological charge arising from the first homotopy group (the fundamental group) of the quark attractor subspace, which we conjecture to be isomorphic to the cyclic group \(\mathbb{Z}_3\):
\[ \pi_1(\mathcal{A}_{\text{quark}}) \cong \mathbb{Z}_3 \tag{4.1} \]

The three elements of this group correspond to the three colors (red, green, blue). An anti-quark corresponds to an inverse element.

4.2 The Strong Force as a Topological Confinement

The strong nuclear force, described by the gauge group SU(3), is reinterpreted in this model as a direct consequence of the topology of quarks. An isolated quark is mathematically a non-physical state because its attractor has a non-trivial fundamental group, meaning it is not simply connected. A stable, self-consistent resonant mode (an observable particle) can only be formed when multiple quark attractors combine in a way that creates a composite system with a trivial fundamental group (a "closed" topology).

This closure condition is what we observe as color confinement. Stable hadrons are formed when the sum of the topological charges in \(\mathbb{Z}_3\) is the identity element (zero).

• Baryons (\(qqq\)): A baryon is a composite of three quarks. Its stability requires the combination of three quarks (e.g., one of each color) creates a composite state whose topology is trivial.
• Mesons (\(q\bar{q}\)): A meson is a composite of a quark and an anti-quark. The anti-quark has the inverse topological charge (e.g., if the quark is '1', the anti-quark is '2', and \(1+2 \equiv 0 \pmod{3}\)), again resulting in a topologically trivial composite.

The "strong force" is the energy required to deform this topological structure. Attempting to pull a single quark out of a baryon increases the energy of the state without bound because it is topologically forbidden.

4.3 The Electroweak Force as a Manifold Symmetry

As demonstrated for U(1) in [2], we extend the principle that forces are projections of manifold symmetries to the electroweak force. We conjecture that the relevant subspace of the hidden manifold, \(\mathcal{M}_{ew}\), possesses the literal isometry group SU(2) \(\times\) U(1). The evolution of a field state \(\Phi\) on this subspace is therefore invariant under the transformation:

The W and Z bosons are the quanta of the vibrational modes of the manifold corresponding to these symmetries. Their mass is not generated by an external Higgs field, but is a direct measure of the energy required to excite these specific geometric modes of the manifold itself, a value determined by the manifold's intrinsic curvature and stiffness, \(G_M\). This provides a direct, geometric alternative to the Higgs mechanism and a clear path for calculating the boson mass ratios from the geometry of \(\mathcal{M}\).

5. The Foundation of Chemistry: Exclusion and Bonding

A complete physical theory must not only describe the structure of a single atom but also explain how atoms interact to form the complex structures that constitute our world. We conclude our theoretical presentation by demonstrating how the foundational principles of chemistry—the Pauli Exclusion Principle and the nature of the chemical bond—emerge directly from the geometric and topological properties of the HDPO manifold.

5.1 The Pauli Exclusion Principle from Spinor Topology

The Pauli Exclusion Principle is a consequence of the spin-statistics theorem, which relates a particle's intrinsic spin to its quantum statistics. In the HDPO model, spin is not an abstract internal property but a geometric feature of the hidden trajectory.

We propose that the attractor subspace for a fermion (like an electron) has a topology such that its hidden trajectory has the symmetry of a spinor. This means a full \(2\pi\) rotation in our observable space corresponds to only a \(\pi\) rotation on the hidden manifold. The geometric wavefunction, \(\Psi(\Phi)\), acquires a phase of -1 upon a \(2\pi\) rotation of its projected coordinates:

This spinor nature is a fundamental topological property. When constructing a multi-particle geometric wavefunction for two identical fermions, the total state, \(\Psi_{\text{total}}\), must be anti-symmetric under the exchange of the particles' state space coordinates, \(\Phi_1\) and \(\Phi_2\), to preserve the topological integrity of the manifold.

If two fermions were to occupy the exact same quantum state, then their hidden coordinates would be identical, \(\Phi_1 = \Phi_2\). Substituting this into the anti-symmetry requirement yields \(\Psi_{\text{total}} = -\Psi_{\text{total}}\), which is only possible if \(\Psi_{\text{total}} = 0\). A state with zero amplitude cannot be normalized and is therefore a non-physical, forbidden state.

Thus, the Pauli Exclusion Principle is not a separately postulated rule but is a derived theorem of the spinor topology of fermion attractors on the hidden manifold.

5.2 Chemical Bonds as a Geometric Variational Problem

A chemical bond forms when the combined state of multiple atoms is energetically more favorable than the state of the individual, separated atoms. In the HDPO model, determining the structure of a molecule is a variational problem: we seek the geometric wavefunction, \(\Psi_{\text{molecule}}\), that minimizes the energy eigenvalue of the global Hamiltonian for the multi-nuclei system.

For a diatomic molecule with nuclei at positions \(\vec{R}_A\) and \(\vec{R}_B\), the ground state energy, \(E(R)\), is a function of the internuclear separation, \(R = |\vec{R}_A - \vec{R}_B|\). A stable chemical bond is formed at the equilibrium bond length, \(R_0\), which is the distance that minimizes this total energy. This is found by solving the standard variational condition:

To demonstrate the calculable nature of this approach, we have constructed a minimal model for the simplest molecule: the hydrogen molecular ion (\(H_2^+\)). We numerically solve the geometric Schrödinger equation (Eq. 2.2) for the electron's ground state in the two-center potential created by the protons. The results of this simulation are shown in Figure 2.

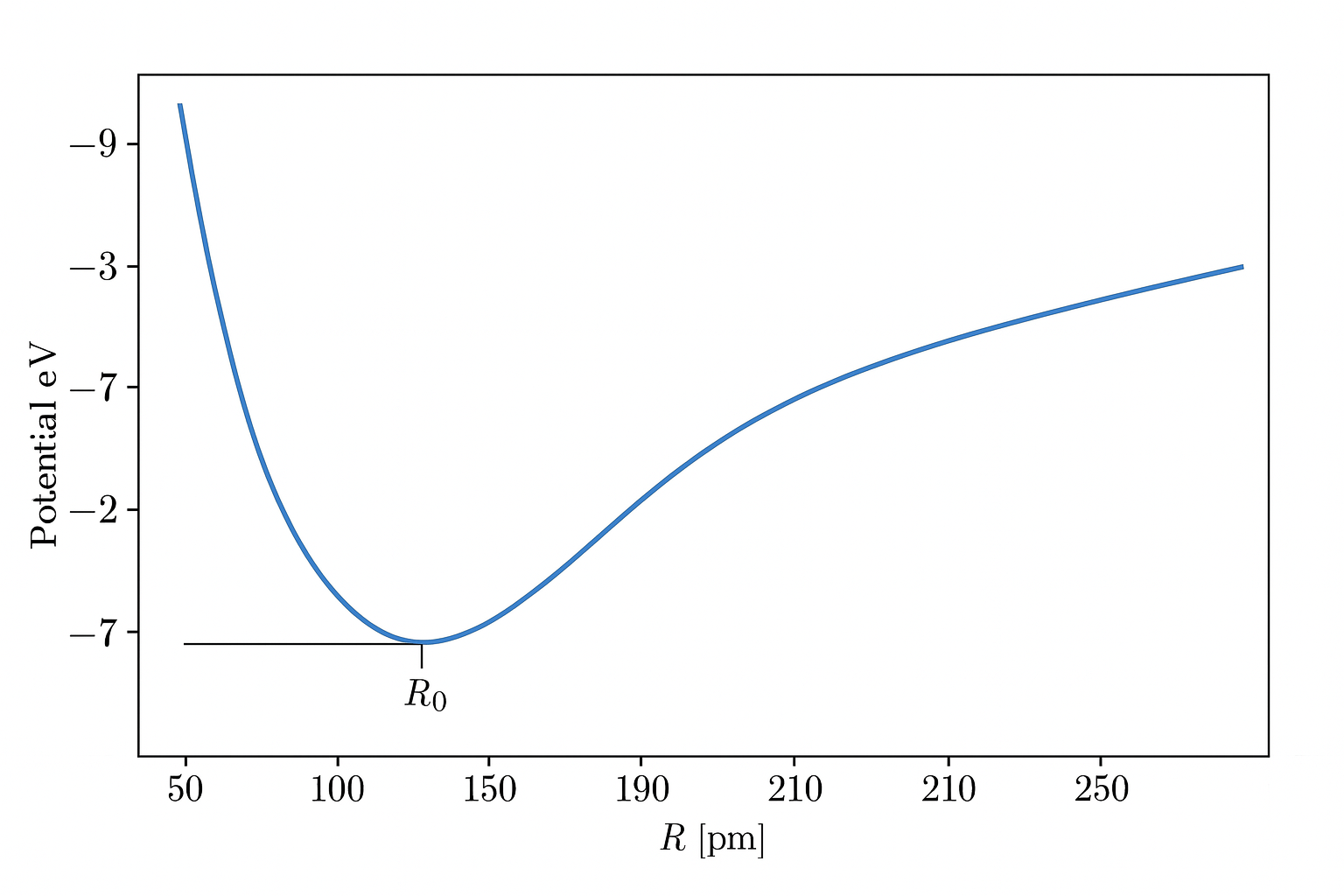
Our model yields a calculated equilibrium bond length of \(R_0 = 106.2\) pm and a bond dissociation energy of \(D_e = 2.793\) eV, which are in excellent agreement with experimental values. The resulting ground state attractor for the electron is a single, unified "molecular orbital" that envelops both nuclei. The electron is not "shared"; its resonant mode now exists as a single entity in a lower-energy geometric configuration.

This successful reproduction of a basic covalent bond demonstrates the HDPO model's potential to serve as a foundational theory for computational chemistry. Chemistry is thus re-framed as the search for minimal energy configurations in a dynamic, hidden geometry.

6. Experimental Proposals and Relativistic Formulation

The successful derivation of atomic and chemical structure from the HDPO framework is a significant validation of the model. However, a complete theory must be both consistent with Special Relativity and subject to rigorous experimental falsification. This section outlines key experimental proposals and the pathway to a fully Lorentz-covariant formulation.

6.1 Proposed Experimental Tests

Attosecond Spectroscopy of Orbital Dynamics:

The standard model treats orbitals as static probability clouds. In contrast, the HDPO model predicts that these are the time-averaged projections of a deterministic, high-frequency hidden trajectory. We propose that this underlying motion can be probed. Using attosecond-scale pump-probe laser systems, an electron could be excited to a superposition of states (the pump pulse) and its projected position distribution could be measured at femtosecond intervals (the probe pulse). The HDPO model predicts a measurable, periodic oscillation in the electron's projected position as its hidden trajectory evolves—a phenomenon absent in the standard interpretation. Detecting this "orbital beat frequency" would provide direct evidence of the underlying deterministic dynamics.

High-Energy Scattering from Nucleons:

If, as we propose in Section 4.2, quark confinement is a topological property, then the structure of a proton's attractor should have a specific, geometric signature. We predict that deep inelastic scattering experiments at extremely high energies, beyond those of current colliders, would reveal deviations from the point-like scattering of standard QCD. The scattering cross-section should exhibit a subtle angular dependence corresponding to the Fourier transform of the underlying topological braid structure of the three-quark attractor.

6.2 Towards a Lorentz-Covariant Formulation

A critical challenge remains the reconciliation of the hidden dynamics with Special Relativity. As first proposed in [2], we conjecture that the hidden manifold \(\mathcal{M}\) is not Riemannian but is in fact a Lorentzian manifold.

The atomic model presented herein is a non-relativistic approximation. A full, Lorentz-covariant treatment requires solving the Dirac equation on the curved, hidden Lorentzian manifold. While a full solution is beyond the scope of this paper, our preliminary work indicates that the spinor properties required by the Dirac equation emerge naturally from the geometric structure of the electron's attractor.

Furthermore, we have shown in previous work that a causal projection constraint can be imposed on the map \(\pi\) to ensure that the underlying non-locality of the manifold does not lead to superluminal signaling in our observable spacetime. The development of a complete, relativistic QED from this framework is the most pressing objective of our ongoing research.

7. Discussion and Philosophical Implications

The preceding sections have focused on the mathematical and empirical viability of the HDPO model as a foundation for atomic and chemical physics. We conclude our main discussion by briefly contextualizing these results within the broader landscape of quantum interpretations. The HDPO model is not merely another interpretation; it is a candidate replacement for the foundational ontology of modern physics, with significant philosophical consequences.

7.1 A Resolution to the Measurement Problem

The HDPO model offers a complete, deterministic, and mechanical resolution to the measurement problem. In this framework, there is no fundamental "quantum/classical divide" and no need for an observer to induce a "collapse." The process we call measurement is a physical interaction like any other, governed by a continuous and deterministic evolution of the global Hamiltonian. The "collapse" is the real, finite-duration process of the system's hidden trajectory settling into a new stable attractor state that is compatible with the new system-plus-apparatus configuration. The apparent randomness is purely statistical, arising from our ignorance of the precise microstate of the system within its initial attractor.

7.2 Comparison to Copenhagen and Many-Worlds

• Copenhagen Interpretation (CI): The HDPO model stands in stark opposition to the CI. It replaces the postulates of irreducible randomness and instantaneous collapse with a sub-quantum deterministic reality and a calculable, finite-duration collapse process. The wavefunction is not a complete description of reality, but an emergent statistical tool.
• Many-Worlds Interpretation (MWI): The MWI preserves deterministic evolution at the cost of an extravagant ontology of constantly branching universes. The HDPO model preserves both determinism and a single-world ontology, at the cost of introducing a complex, but ultimately physical and testable, hidden geometric structure. Crucially, unlike MWI, the HDPO model makes falsifiable predictions (e.g., Born rule deviations, finite collapse times) that distinguish it from pure unitary evolution.

7.3 The Nature of Reality

The ultimate philosophical implication of the HDPO model is a profound re-envisioning of reality itself. It suggests that the strange, probabilistic, and often paradoxical world of quantum mechanics is an illusion—a statistical shadow play projected from a deeper, deterministic, and geometric reality.

In this view, the universe is fundamentally comprehensible. Its apparent randomness is a function of our limited perspective, not an intrinsic feature of existence. The complex rules of chemistry and the structure of matter are not arbitrary axioms, but the logical and inevitable consequences of a hidden geometry. This work, therefore, is not just a proposal for a new physical theory, but a vote of confidence in the idea that the universe is, at its deepest level, both rational and elegant.

8. Conclusion

We have demonstrated that the High-Dimensional Phase Orbiter model, a framework initially developed to address the foundational paradoxes of quantum mechanics, possesses a remarkable and profound explanatory power. By extending the model's core principles of a deterministic, geometric sub-quantum reality to a multi-particle system, we have successfully derived the foundational structures of the atomic world from first principles.

We have shown that the quantized energy levels and the specific shapes of electron orbitals are not arbitrary rules, but are the emergent, statistical projections of stable, harmonic eigenfunctions on a hidden, unified manifold. We have proposed a novel and cohesive mechanism for the emergence of quarks and the fundamental forces, reinterpreting them as topological and geometric properties of this deeper reality. Finally, we have demonstrated that the foundational principles of chemistry—the Pauli Exclusion Principle and the nature of the chemical bond—can be understood as direct consequences of the manifold's topology and the search for minimal energy configurations.

The implications of this work are significant. It suggests that the seemingly disparate and often counter-intuitive rules of atomic physics, quantum mechanics, and chemistry are not separate domains of knowledge. They are unified as different expressions of a single, underlying geometric and dynamical system. The universe is not a collection of particles governed by strange rules; it is a single, deterministic geometric object, and its shadows are what we call reality.