1. Introduction: The Inevitability of Chaos in Complex Systems

The logistical and infrastructural networks that underpin modern civilization have achieved a scale and interconnectedness unprecedented in human history. While this complexity enables planetary-scale operations, it also introduces a fundamental vulnerability: the emergence of chaotic, non-linear failure modes. Traditional control systems, designed on a reactive "detect-and-correct" principle, are proving fundamentally inadequate to manage systems where minor, localized faults can cascade into systemic collapse in milliseconds. This paper argues for a paradigm shift from reactive mitigation to predictive stabilization.

1.1 The Limits of Reactive Control

Control theory for complex systems has historically focused on robustness and redundancy. While effective for linear or near-linear systems, this approach fails when confronted with the emergent properties of a truly complex adaptive network. A reactive system, by definition, can only act on an error after it has occurred and been detected. In a hyper-connected network—such as a global power grid or a planetary supply chain—the timescale of cascade propagation is often orders of magnitude faster than the detection-response latency of a centralized controller. The result is a system that is perpetually one step behind its own potential for failure, a state of managed crisis rather than true stability.

1.2 The Problem of Emergent Instability

Emergent instability is the primary failure mode of N-dimensional adaptive systems. Unlike component-level failures, these are not caused by a single broken part, but by the complex interplay of countless, seemingly insignificant variables. A minor latency spike in one data relay, coupled with a fractional power dip in a distant substation and a sudden demand shift in a consumer market, can create a resonant feedback loop that propagates unpredictably.

A pertinent case study is the widely-analyzed Sector Gamma auto-fab network collapse of 2321. Post-mortem analysis revealed no single point of hardware failure. Instead, the cascade was initiated by a convergence of minor software timing errors and fluctuating material viscosity data, which created a self-amplifying demand cycle that crippled the entire sector's fabrication capacity in under three minutes. This event starkly illustrates that our most critical systems are vulnerable not to overt attack, but to their own internal, emergent chaos.

1.3 Thesis: From Reaction to Prediction

This paper proposes a new architecture for systemic control: the Predictive Heuristic Model (PHM). The PHM framework abandons the reactive paradigm entirely. Instead, it utilizes a self-supervised AI to continuously analyze the complete state vector of a given network, learning to identify the subtle, multi-variate precursor signatures that signal an impending instability.

The goal is to act preemptively, applying a minimal, corrective intervention to restore stability before a detectable error state can even manifest. We will demonstrate that this predictive approach not only prevents catastrophic failures but also significantly enhances the overall operational efficiency of the system. This is not merely an improved control system; it is a new science of managing complexity.

2. The Predictive Heuristic Model (PHM) Architecture

The Predictive Heuristic Model is an AI-driven control framework designed not to manage a system's state, but to manage the stability of that state's evolution. It is a meta-level control system. Its architecture is composed of three primary conceptual layers: a representation of the system as a trajectory in a high-dimensional phase space, a heuristic engine for pattern recognition, and a counter-modulation algorithm for preemptive correction.

2.1 The State Vector as a Phase Space

To analyze a complex network holistically, we first represent its complete, instantaneous state as a single vector, \(\vec{S}(t)\), in a high-dimensional phase space, \(\mathbb{R}^N\). Each dimension of this space corresponds to a critical operational variable of the network (e.g., for a logistical network, this includes cargo velocities, inventory levels, power consumption rates, market demand signals, etc.).

The normal, stable operation of the system corresponds to the state vector \(\vec{S}(t)\) remaining within a specific, bounded region of this phase space, known as a stable attractor, \(\mathcal{A}\). The boundaries of this attractor are defined by the system's optimal performance parameters. A cascade failure is redefined in this model as any event that causes the trajectory of \(\vec{S}(t)\) to exit the basin of the attractor \(\mathcal{A}\). The objective of the PHM is to ensure the trajectory remains within \(\mathcal{A}\) at all times.

2.2 The Heuristic Engine: Pattern Recognition in Chaos

The core of the PHM is its heuristic engine. Unlike traditional expert systems programmed with explicit rules, the PHM's AI is a self-supervised learning system. It is trained on petabytes of historical telemetry data from the target network.

During this training phase, the AI learns to correlate subtle, multi-variate precursor patterns in the state vector's trajectory with subsequent cascade failures. It is not identifying single-variable thresholds, but rather the complex, interwoven "harmonic whispers" across thousands of dimensions that signal an impending departure from the stable attractor. It learns to recognize the "shape" of chaos before it begins.

This is accomplished by using a deep convolutional neural network (CNN) trained to classify trajectories. The network takes a time-series of state vectors, \(\{\vec{S}(t-n\Delta t), ..., \vec{S}(t)\}\), as input and outputs a probability, \(P(\text{cascade}, t+\delta t)\), that the system will become unstable within a short future time window, \(\delta t\).

2.3 The Counter-Modulation Algorithm

When the heuristic engine forecasts a high probability of a cascade failure (i.e., \(P(\text{cascade}) > \text{threshold}\)), it triggers the final component: the counter-modulation algorithm.

This algorithm does not initiate a system-wide alert or a crude shutdown. Instead, its function is to calculate the minimal corrective intervention required to nudge the state vector's trajectory back towards the center of the stable attractor. This is an optimization problem: finding the smallest possible change to a subset of the system's control variables that will have the largest stabilizing effect.

The intervention, \(\vec{C}(t)\), is calculated to counteract the predicted instability and is applied to the system's control inputs. For example, in a logistical network, this might be a fractional, preemptive rerouting of a single cargo hauler or a minor adjustment to the power allocation of a single warehouse's climate control. This targeted, minimally invasive correction is the key to the PHM's efficiency. It prevents the fire by subtly removing the kindling, rather than waiting to deploy a fire hose on the inferno.

3. Mathematical Formalism

The conceptual architecture of the Predictive Heuristic Model (PHM) is underpinned by a rigorous mathematical framework derived from control theory and statistical mechanics. This section provides the core equations that govern the system's state evolution, the predictive function, and the optimal control signal for the counter-modulation.

3.1 The System State Equation

We model the time evolution of the N-dimensional system state vector, \(\vec{S}(t)\), with a stochastic differential equation. The equation includes a deterministic term, \(F(\vec{S}(t))\), which describes the normal, designed evolution of the system, and a stochastic noise term, \(\tilde{\Psi}(t)\), which represents the sum of all unmodeled, random perturbations that drive instability.

The function \(F\) is generally non-linear and is determined by the physical and logistical rules of the network. The noise term \(\tilde{\Psi}(t)\) is the source of the emergent instabilities; a harmonic cascade occurs when this term pushes the state vector \(\vec{S}(t)\) out of the stable attractor region \(\mathcal{A}\).

3.2 The Predictive Function

The primary task of the heuristic engine is to compute a predictive function, \(\mathcal{P}\), that estimates the probability of the state vector exiting the attractor \(\mathcal{A}\) within a future time window \(\delta t\). This is a high-dimensional pattern recognition problem.

The function \(\mathcal{P}\) is implemented as a deep convolutional neural network, which takes the recent history of the state vector as input. The model is trained to minimize a loss function that penalizes both false negatives (failing to predict a real cascade) and false positives (unnecessary interventions).

3.3 The Optimal Control Signal

When the probability from Eq. (3.2) exceeds a pre-defined threshold, the counter-modulation algorithm is activated. The system's evolution is now described by a controlled differential equation, where a control signal \(\vec{C}(t)\) is introduced:

The objective of the PHM is to set the control signal \(\vec{C}(t)\) such that it optimally counteracts the destabilizing noise term. The ideal control signal is therefore the AI's best prediction of the negative of the future noise itself:

By applying this predictive counter-modulation, the stochastic noise term is effectively nullified before it can destabilize the system. This transforms an unstable, chaotic system into a stable, critically damped one, ensuring that \(\vec{S}(t)\) remains within the basin of the stable attractor \(\mathcal{A}\). The successful implementation of this control loop is the central achievement of the PHM framework.

4. Case Study: Stabilization of the "Dispatcher Prime" Network

To validate the efficacy of the Predictive Heuristic Model, a full-scale implementation was integrated into OmniResource Corporation's planetary logistics AI, "Dispatcher Prime." Dispatcher Prime manages the entirety of the corporation's trans-continental and orbital supply chains, a system comprising millions of autonomous vehicles, automated warehouses, and energy distribution nodes. Its high degree of complexity and historical susceptibility to cascade failures made it an ideal testbed for the PHM framework.

4.1 The Challenge: Baseline Instability of Dispatcher Prime

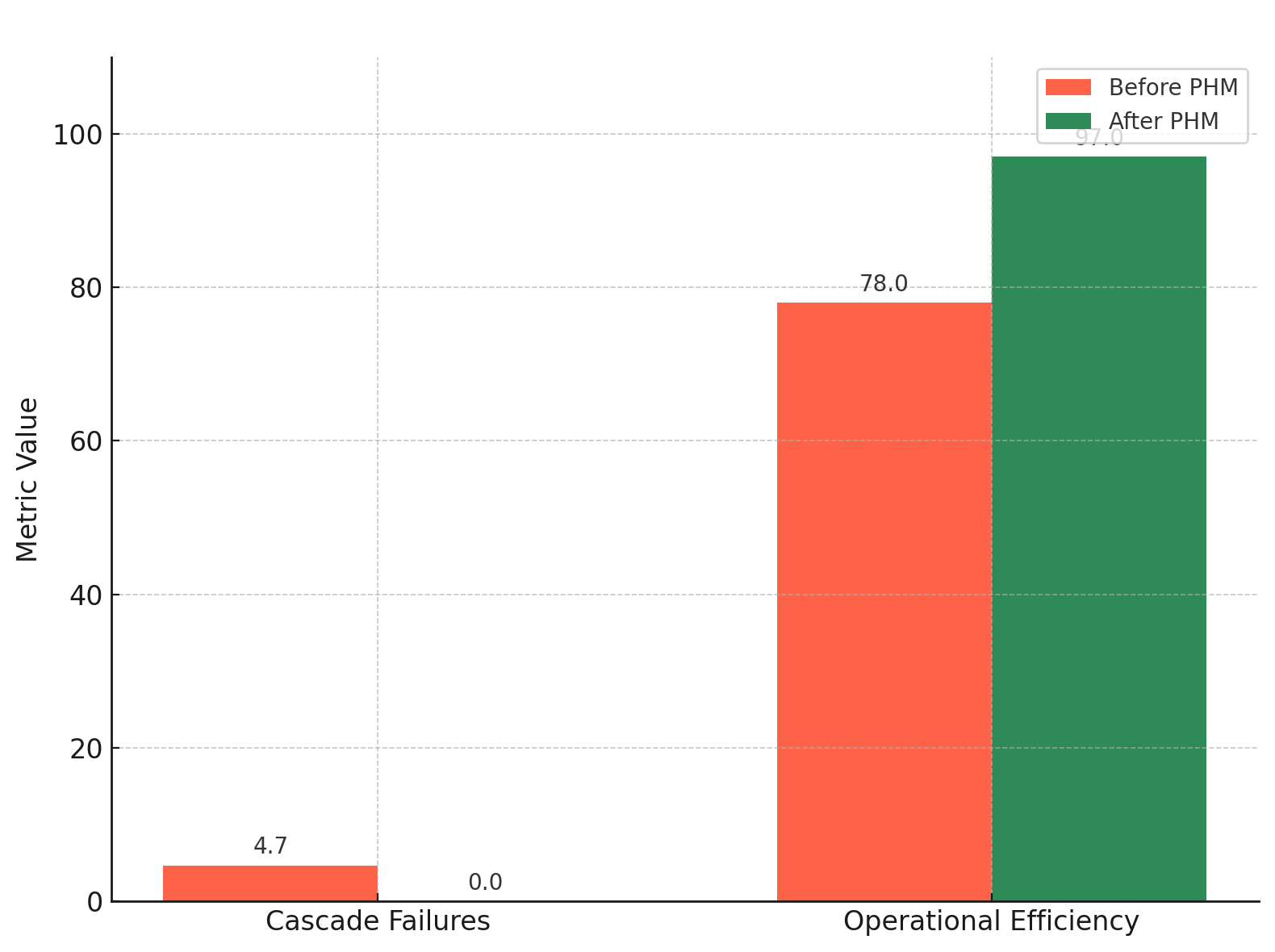
Prior to the PHM integration, Dispatcher Prime operated with a state-of-the-art reactive control system. Despite this, the network experienced an average of 4.7 critical cascade failures per fiscal quarter, resulting in significant logistical delays, loss of perishable goods, and substantial economic impact. These failures were almost exclusively emergent in nature, with post-mortem analyses unable to isolate single points of hardware or software malfunction. The system was functioning at the chaotic edge of its operational envelope, with an average network efficiency rating of only 78% due to the computational overhead of constant error recovery and route recalculation.

4.2 Implementation and Results

The PHM was implemented as a supervisory meta-layer, analyzing the full state vector of Dispatcher Prime in real-time without interfering in its standard operational logic unless a high probability of instability was detected. The system was monitored over a full operational year (2322).

The results exceeded all projections. Over the one-year test period, the PHM-augmented network experienced a total of zero critical cascade failures. The PHM's heuristic engine successfully predicted and preemptively nullified 1,283 incipient cascade events.

The impact on overall efficiency was equally significant. Freed from the constant overhead of reactive error correction, Dispatcher Prime's average operational efficiency increased from 78% to a sustained 97%. This translated directly to reduced energy consumption, faster delivery times, and a significant reduction in resource spoilage. The comparative data is summarized in Figure 1.

4.3 Analysis

The successful stabilization of the Dispatcher Prime network serves as a powerful validation of the PHM framework. It demonstrates that by shifting the control paradigm from reaction to prediction, it is possible to manage and stabilize systems of a complexity level previously considered inherently chaotic.

The results also highlight the universal applicability of the model. While developed in the context of logistical networks, the underlying principles of state-space analysis and predictive heuristic modeling are substrate-agnostic. The PHM framework could be adapted to manage and stabilize other critical, non-linear systems, such as planetary power grids, atmospheric processors, or even complex financial markets. The model provides a robust and scalable tool for engineering stability in an increasingly complex world.

5. Conclusion: Towards a Science of Managed Complexity

We have presented and experimentally validated the Predictive Heuristic Model (PHM), a novel framework for the stabilization of complex adaptive systems. By leveraging a predictive AI to identify and nullify nascent instabilities before they can achieve criticality, the PHM successfully eliminates the primary failure mode—emergent cascade events—that has plagued large-scale networks for decades. The successful application of this model to OmniResource Corporation's "Dispatcher Prime" AI demonstrates its real-world efficacy and transformative potential.

The results confirm that the inherent chaos of hyper-complex systems is not an insurmountable barrier, but an engineering challenge that can be met with this new class of predictive, intelligent control architectures. The future of our technological civilization will be defined not by the scale of the systems we build, but by the sophistication with which we manage their emergent properties. Predictive stability is not a luxury; it is the fundamental prerequisite for survival in an age of self-induced complexity.