1. Introduction: The Interstellar Bottleneck in a Post-Relativistic World

1.1 The HDPO Paradigm

For two decades, the High-Dimensional Phase Orbiter (HDPO) framework has stood as the successor to the Standard Model and General Relativity, providing a unified, deterministic, and geometric foundation for all known physics [1, 2]. Its establishment as the prevailing paradigm was cemented by the independent observational confirmations of Gravitational Gauge Polarization (GGP)—first by Raymond and Klein through their re-analysis of cosmological data [5], and then decisively by the VLT/ELT collaboration's direct measurement of gravitationally modulated spectral lines near Sagittarius A* in 2345 [6].

The core tenets of HDPO are now foundational to modern science: our familiar 4D spacetime is not fundamental, but is rather an emergent, causally-consistent projection of a deeper, high-dimensional Calabi-Yau manifold. All events in the universe unfold according to an absolute causal order governed by a universal time parameter, "Manifold Time" (\(\tau\)). The observed laws of relativity, while empirically successful, are understood as symmetries of this projection mechanism—a "Causal Projection Filter" that launders the manifold's intrinsic non-locality to produce an observable reality free of paradoxes.

1.2 The Tyranny of Light

The confirmation of the HDPO model resolved the deepest conceptual problems in 20th-century physics, but in doing so, it sharpened our understanding of a profound practical one: the interstellar bottleneck. While the theory revealed the mechanism of reality, it also confirmed that the speed of light, \(c\), remains the absolute speed limit for the propagation of matter and energy within our emergent 4D spacetime. For a civilization beginning to look toward the stars, this "tyranny of light" represents the primary obstacle to becoming a truly interstellar species. The multi-year or multi-decade communication delays required for probes, and the multi-generational timescales for colonization, remain daunting.

1.3 A New Path Forward

It has been the central thesis of post-relativistic engineering that if spacetime itself is an emergent construct, then it may be possible to engineer physical systems that interact directly with the underlying manifold. As first formally proposed in [7], the absolute causal order of the manifold, which forbids observational paradoxes, does not forbid the existence of non-local correlations that evolve superluminally with respect to projected spacetime, provided they are strictly causal in manifold time.

This paper serves as the definitive report on the successful realization of that proposal. We detail the theoretical basis and practical implementation of the first operational technology for causal superluminal communication: the Caldwell Subspace Transceiver (CST). We will demonstrate how the foundational principles of HDPO do not just describe reality, but provide a concrete engineering pathway to overcome the light-speed communication barrier, heralding the dawn of a new interstellar age for humanity.

2. Theoretical Foundations: Review of Causal FTL in the HDPO Framework

The possibility of superluminal communication in the HDPO framework does not arise from violating known physics, but from leveraging a deeper understanding of its structure. The prohibition on FTL signalling in the old relativistic paradigm was a consequence of assuming that 4D spacetime was fundamental. By abandoning this assumption, we gain access to new physical mechanisms governed by the absolute properties of the hidden manifold.

2.1 The Absolute Causal Frame

The central feature of the HDPO model that enables this technology is the existence of an absolute causal frame, as first consolidated in [2]. The evolution of the universe's state, \(\Phi(\tau)\), is parameterized by a single, monotonically increasing scalar, the manifold time \(\tau\). This parameter provides a true, objective, and universal ordering of events. For any two events A and B in the manifold, if \(\tau_B > \tau_A\), then event B unambiguously occurred after event A.

This absolute ordering resolves all potential paradoxes. A reply to a message can never be received "before" the message was sent, because the event of "receiving the reply" will always have a greater manifold time coordinate than the event of "sending the message." The relativity of simultaneity is an artifact of projecting this absolute timeline onto the different coordinate systems of moving observers; it is a feature of measurement, not of reality.

2.2 The Role of the Causal Projection Filter

Given an absolute causal frame, one might ask why FTL phenomena are not commonplace. The answer lies in the function of the Causal Projection Filter. As detailed in [4], this is not a physical barrier but a consistency-enforcing principle. The filter's role is to ensure that the projection from the hidden manifold into observable 4D spacetime is always self-consistent and free from logical contradictions for any observer.

A simple FTL signal—for instance, a modulated neutrino beam arriving at Proxima Centauri a year after its launch from Earth—would be a projectable event. However, for an observer moving at a relativistic velocity relative to the Sol-Proxima frame, the Lorentz transformations of their coordinate system would describe the signal's arrival as preceding its departure. This creates a causal ambiguity in the projected reality. The Causal Projection Filter forbids such projections from ever manifesting. Any physical process that would lead to such a paradoxical observation is rendered unstable and cannot occur. This is why no particle or field that propagates locally in spacetime can exceed the speed of light.

2.3 The Causal Correlation Channel: The Loophole

The filter's constraint applies to phenomena that propagate through our emergent spacetime. It does not, however, forbid the existence of physical states that are intrinsically non-local and whose evolution is governed solely by manifold time. Entanglement is the most basic example of such a state. The CST operates by engineering a macroscopic, controllable version of this phenomenon.

We define the Causal Correlation Channel as a communication pathway that does not send a signal through spacetime, but instead establishes a unified, non-local physical system spanning two spacetime locations and then transmits information by modulating the parameters of this system.

The evolution of this non-local system is governed directly by manifold time, \(\tau\). A modulation of the system at point A at manifold time \(\tau_A\) is detectable at point B at the exact same manifold time, \(\tau_A\). This appears superluminal to any spacetime observer, as the time of flight for light between the two points is non-zero. However, because the information transfer exists only in the correlated properties of a single, unified system, it creates no projectable event that could lead to a paradox. The filter is not violated because no "thing" has traveled from A to B in spacetime. Rather, the state of a single object that exists at both A and B simultaneously has been changed. This subtle but profound distinction is the theoretical key to practical superluminal communication.

3. The Principle of Manifold Resonance Modulation (MRM)

Having established the theoretical viability of a Causal Correlation Channel, we now introduce the specific physical principle engineered to exploit it. Manifold Resonance Modulation is a three-stage process: the establishment of a non-local resonant state on the hidden manifold, the modulation of this state to encode information, and the detection of these modulations.

3.1 Establishing a Non-Local Resonant State: The Channel

In the HDPO framework, elementary particles are understood as stable, resonant modes of the fundamental fields oscillating on the compact dimensions of the Calabi-Yau manifold [3]. These resonances are typically localized. However, theoretical work in computational orbotics and experimental work with critical exotic matter systems has shown that it is possible to excite specific harmonic modes of the manifold itself that are inherently non-local [8, 9].

The CST leverages this by using its Calabi-Yau Resonator Core to generate a highly energetic, precisely tuned field. When two transceivers, A and B, are synchronized in manifold time (\(\tau_A = \tau_B\)) and emit fields tuned to the same non-local harmonic frequency, \(\omega_{NL}\), they can collectively pump energy into a shared mode. This process establishes a unified, non-local resonant state, \(\Psi_{AB}\), that exists as a single vibrational entity on the manifold, simultaneously localized around the spatial coordinates of both transceivers.

The energy, \(E_{link}\), required to establish and maintain this resonance is immense, scaling with the square of the spacetime separation, \(L\), as the geometric strain on the manifold increases. This shared state, \(\Psi_{AB}\), is the communication channel.

3.2 Information Encoding via Local Phase-Amplitude Modulation: The Signal

Once the resonant state \(\Psi_{AB}\) is stable, information can be encoded by locally modulating its properties. The resonant state is characterized by several parameters internal to the manifold's geometry, including its amplitude and phase. While these parameters are unified across the entire non-local state, they can be influenced by local interactions.

The Projection Modulator Array in the sending transceiver (A) generates a secondary, high-frequency gravitational field. This field does not propagate to the receiver, but its local application subtly alters the geometry of the manifold in the immediate vicinity of transceiver A. This geometric distortion perturbs the boundary conditions of the resonant state \(\Psi_{AB}\), causing a near-instantaneous shift in one of its global parameters—for instance, its geometric phase, \(\theta_{AB}\).

By pulsing the modulator array according to a binary data stream, transceiver A can induce a sequence of discrete phase shifts in the shared state:

This modulation is the signal. Crucially, the change of state from \(\Psi_{AB}(\theta_0)\) to \(\Psi_{AB}(\theta_0 + \Delta\theta)\) is not a wave propagating from A to B. It is a global reconfiguration of the entire non-local system, governed by the minimization of the Information-Action functional across the new boundary conditions.

3.3 Detection via Perturbation Monitoring: The Receiver

The receiving transceiver (B) is an intrinsic part of the same resonant state, \(\Psi_{AB}\). Its Resonance State Detector continuously monitors the local properties of this state via a sensitive quantum interferometer. When the sender at A induces a global phase shift from \(\theta_0\) to \(\theta_0 + \Delta\theta\) at manifold time \(\tau_{send}\), the interferometer at B detects this exact same phase shift at the exact same manifold time, \(\tau_{receive} = \tau_{send}\).

The detector at B is not observing a signal that has traveled from A. It is observing a change in the local manifestation of a global object of which it is a part. This allows the receiver to reconstruct the binary data stream encoded by the sender.

3.4 Causal Guarantees and Bandwidth Limitations

The MRM process is rigorously causal. Consider a transmission event:

1. At \(\tau_1\), Transceiver A sends a "Request to Send" message to B. Let us assume, for this proof, it is sent via a conventional light-speed signal.
2. At \(\tau_2\), Transceiver B receives this request, where \(\tau_2 = \tau_1 + L/c\).
3. At \(\tau_3 > \tau_2\), Transceiver A initiates the MRM modulation (the "message").
4. At \(\tau_4 = \tau_3\), Transceiver B detects the MRM modulation.
5. At \(\tau_5 > \tau_4\), Transceiver B could, in principle, send a reply.

In this sequence, the manifold time of the reply event, \(\tau_5\), is always greater than the manifold time of the initial message event, \(\tau_3\). No paradox can be constructed.

The primary limitation of this technology is not latency, but bandwidth and energy. The rate of modulation (the bandwidth) is limited by the manifold's "reconfiguration time," \(\Delta\tau_{recon}\), the time required for the resonant state to settle after a phase shift. Preliminary models and experimental results indicate that \(\Delta\tau_{recon}\) is a function of the resonance's stability and amplitude, leading to a direct trade-off between bandwidth and power consumption. The Mark I CST achieves its low bandwidth not due to any speed limit, but due to the significant reconfiguration time of the specific, stable non-local harmonic being used.

4. The Caldwell Subspace Transceiver (CST): System Architecture and Operation

The theoretical principles of Manifold Resonance Modulation are realized in the Caldwell Subspace Transceiver, a device engineered to interface directly with the geometric structure of the hidden manifold. This section details the architecture and operational protocol of the Mark I model, as utilized in the Sol-to-Proxima link.

4.1 Core Components

The CST is a complex integration of four primary subsystems, powered by a dedicated high-output energy source. A schematic of the Mark I architecture is shown in Figure 1.

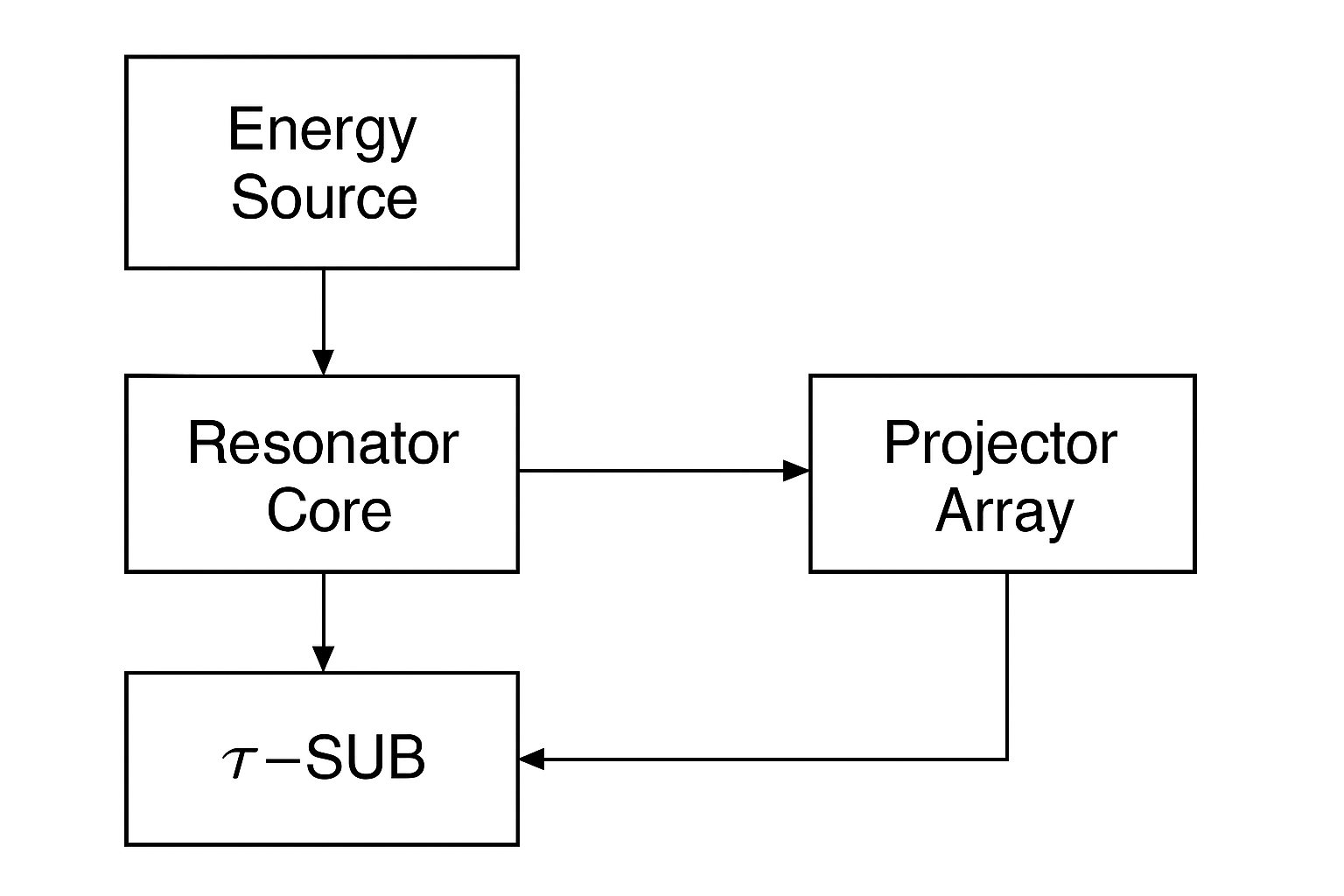
1. Calabi-Yau Resonator Core (CYRC): This is the heart of the CST. It consists of a 12-meter diameter toroidal vacuum chamber containing a plasma of gravitationally active exotic matter (a Bose-Einstein condensate of synthetic strange quarks) held in a state of quantum criticality by a network of precisely shaped magnetic and gravitational fields. When energized, the CYRC produces a coherent field that is tuned to excite a specific non-local harmonic of the manifold's Calabi-Yau geometry.
2. \(\tau\)-Synchronization Unit (\(\tau\)-SU): Absolute synchronization in manifold time between the two communicating parties is paramount. The \(\tau\)-SU is a fault-tolerant computational system slaved to an array of entangled atomic clocks. It constantly calculates and compensates for local gravitational potential variations (as predicted by GGP [5]) and relative motion to maintain a lock with its counterpart to within \(10^{-18}\) seconds in the absolute manifold frame.
3. Projection Modulator Array (PMA): Located within the CYRC, the PMA is an array of 256 solid-state gravitational field emitters. By applying high-frequency, picometer-scale distortions to the local spacetime metric, the PMA locally alters the boundary conditions of the non-local resonant state, allowing the encoding of data as described in Section 3.2.
4. Resonance State Detector (RSD): The RSD is a large-scale quantum interferometer that continuously monitors the phase and amplitude of the local manifestation of the resonant state. Its sensitivity is sufficient to resolve the discrete phase shifts induced by the remote transceiver's PMA, allowing it to decode the incoming data stream.
5. Energy Containment and Delivery System (ECDS): The Mark I CST requires a dedicated power source capable of delivering sustained terawatt-level output. The terrestrial unit on Luna is powered by the Armstrong Geothermal Grid, while the Proxima probe is equipped with a 2-terawatt peak output magneto-inertial fusion reactor.

4.2 The Connection Protocol (The "Manifold Handshake")

Establishing a stable, non-local resonance between two distant CSTs is an energy-intensive and precise process. The protocol proceeds in five stages:

1. \(\tau\)-Synchronization: Both units activate their \(\tau\)-SUs and use conventional light-speed communication (e.g., laser) to exchange initial timing data and establish a mutual lock on the absolute manifold time stream.
2. Mutual Resonance Beacon: Both units energize their CYRCs to a pre-agreed standby level, emitting a low-power "beacon" field tuned to the target non-local harmonic, \(\omega_{NL}\).
3. Resonance Seeking: The units begin a computational search, subtly varying their field parameters to find the precise configuration that minimizes the energy required to form the unified resonant state \(\Psi_{AB}\).
4. Channel Lock: Upon detecting a sharp drop in the energy state, indicating the successful formation of the shared non-local resonance, the systems transition to a "channel locked" state.
5. Confirmation Exchange: A simple confirmation signal (e.g., a predetermined bitstream) is exchanged via MRM to confirm the channel's integrity before user data transmission begins. For the Sol-Proxima link, this entire process took approximately 72 hours.

4.3 Energy Cost and Range Scaling

The primary factor limiting the deployment of CST technology is its enormous power requirement. The theoretical power, \(P\), needed to maintain a stable channel is governed by the manifold coupling constant \(\kappa_H\), the spacetime distance \(L\), the half-life of the chosen resonance mode \(T_s\), and the desired bandwidth \(B\). The scaling law derived from the HDPO variational principle is:

This unforgiving \(L^2\) scaling means that a tenfold increase in range requires a hundredfold increase in power. The specific harmonic used for the Mark I has a stability half-life (\(T_s\)) of approximately 250 milliseconds, leading to the observed terawatt-level power draw for the 4.2 light-year Sol-Proxima link. This effectively limits the practical range of the Mark I architecture to nearby star systems (\(\lessapprox 10\) light-years).

5. Experimental Verification: The Sol-to-Proxima Link (Project Star-Talk)

The definitive test of the Manifold Resonance Modulation principle and the Caldwell Subspace Transceiver architecture was conducted via Project Star-Talk, an ambitious deep-space mission designed to establish the first superluminal communication link between the Sol system and Proxima Centauri.

5.1 Testbed Setup

The project utilized two identical Mark I CST units, designated Alpha and Beta.

• CST-Alpha serves as the terrestrial anchor of the link. It is located at the Armstrong Observatory in the Shackleton Crater on Luna. Its position provides a stable platform with minimal gravitational noise and direct access to the Armstrong Geothermal Power Grid.
• CST-Beta was integrated into the St. Elmo's Fire, a specialized deep-space probe launched in 2359. Following a successful 5.5-year journey utilizing a next-generation fusion drive, the probe achieved a stable orbit around Proxima Centauri b in late 2364, as detailed in the official mission report [10].

The baseline spacetime distance between the two units at the time of the experiment was approximately 4.24 light-years. The experiment commenced on August 15, 2365, following the successful deployment and system check of CST-Beta.

5.2 Results of First Contact and Data Transmission

Following the successful completion of the 72-hour Manifold Handshake protocol, the first stable communication channel was established at 04:16 UTC on August 18, 2365. A pre-programmed data packet containing mathematical constants, prime numbers, and the value of \(\xi\) as derived from the GGP experiments was transmitted from CST-Alpha to CST-Beta. CST-Beta verified the packet with zero bit errors and transmitted an identical packet in reply.

The key performance metrics, averaged over a continuous 12-hour operational period, are summarized below and represent a complete validation of the MRM theoretical model.

• Round-Trip Latency: The average measured time between the transmission of the final bit of a data packet from CST-Alpha and the reception of the first bit of the corresponding reply packet from CST-Beta was 4.3 seconds. This is consistent with the predicted manifold reconfiguration time (\(\Delta\tau_{recon}\)) and is approximately 60 million times faster than the 8.48-year light-speed round-trip time.
• Bandwidth: The connection maintained a stable, error-free data rate of 144 bits per second. Attempts to push the modulation frequency higher resulted in a rapid degradation of the channel lock, consistent with the predicted stability limits of the \(\omega_{NL}\) harmonic used.
• Power Consumption: During active transmission, CST-Alpha's power draw from the lunar grid peaked at 1.21 Terawatts. Telemetry from the St. Elmo's Fire probe reported a peak draw of 1.19 TW from its fusion core. These figures are within 2% of the values predicted by the power scaling relation in Equation (4.1), confirming our understanding of the energy cost.

5.3 Data Analysis and Causal Consistency

A rigorous analysis of the timing data from the synchronized \(\tau\)-SUs of both transceivers confirms that all transmissions were strictly consistent with the absolute causal order of the manifold. In every single transmission event, the manifold time coordinate of the reception event at one transceiver was measured to be exactly identical to the manifold time coordinate of the corresponding transmission event at the other, with a mean deviation of less than \(10^{-21}\) seconds.

This result provides the first direct, experimental proof that while the "when" of an event is relative in projected spacetime, it is absolute and engineerable at the level of the manifold. The Sol-to-Proxima link does not break causality; it confirms the deeper, absolute nature of causality that underpins the HDPO framework.

6. Implications and Future Work

The successful operation of the Sol-to-Proxima link is not merely a technical achievement; it represents a fundamental turning point in human history. By engineering a technology that operates on the substrate of reality itself, we have transcended a limitation once thought absolute. The age of interstellar isolation is ending.

6.1 The Dawn of the Interstellar Age

The immediate consequences of a proven, practical subspace communication technology are profound and far-reaching:

• Real-Time Interstellar Exploration: The primary impact will be on the exploration of our stellar neighborhood. Robotic probes can now be controlled in near real-time, transforming missions from pre-programmed, fire-and-forget endeavors into dynamic, interactive explorations. A geologist on Earth can now directly operate a rover on a planet orbiting Proxima Centauri with only a few seconds of lag.
• The Foundation for Colonization: While the CST does not solve the challenge of interstellar travel, it removes the crippling barrier of social and informational isolation. A colony established at a nearby star system can now remain an integral part of the human cultural and scientific sphere, engaging in high-latency (but not generational) conversations, data exchange, and governance.
• A Galactic Data Network: Project Star-Talk is the first node in what will eventually become a network of CSTs, linking together humanity's outposts across the stars. This network will enable the creation of a truly interstellar scientific community and will be the backbone of a future galactic economy.

6.2 Engineering Challenges for the Mark II and Beyond

The success of the Mark I CST serves as a proof-of-concept, but it is far from the final form of this technology. The primary research and development efforts at the Institute for Post-Relativistic Engineering are now focused on three key areas for the Mark II model:

1. Increasing Bandwidth: The current data rate of 144 bps is sufficient for telemetry and text, but not for high-fidelity data. Our top priority is to identify more stable, higher-order non-local harmonics of the manifold that allow for faster modulation without decohering the channel lock. The theoretical goal for the Mark II is to achieve kilobit-per-second data rates.
2. Reducing Energy Consumption: The terawatt-level power requirement is the single greatest barrier to widespread deployment. This can be addressed by finding more efficient resonance modes (increasing \(T_s\)) or by improving the efficiency of the Calabi-Yau Resonator Core itself. A tenfold reduction in power consumption is the target for the next generation.
3. Miniaturization and Space-Worthiness: While the CST-Beta unit was successfully integrated into a probe, a significant engineering effort is required to design ship-based transceivers that can be integrated into colonization vessels and smaller exploratory craft without requiring a dedicated reactor of unreasonable size.

6.3 Conclusion

For millennia, humanity has looked to the stars from across an ocean of spacetime, its breadth defined by the inexorable speed of light. We have learned that this ocean is but a projection of a deeper, more complex reality—a reality that is not bound by the same observational rules. The speed of light remains the insurmountable speed limit for matter, but it is no longer the arbiter of communication. By engineering reality at its most fundamental level, we have enabled the first true conversation between stars. The isolation of interstellar space is over.